Simulation de la multiplication – Bac théorique – Section informatique – 2018

Sujet (Algo et programmation - Bac 2018)
On se propose de simuler la multiplication de deux entiers naturels A et D (avec A et H dans 110, 10000j), en utilisant ]a méthode du mathématicien Ibn Al Barna comme suit
a.) Former deux chaînes CA et CB contenant respectivement, les chiffres de l'entier A et les chiffres de l'entier B.
b) Ajuster la longueur des deux chaîne CA et CB en complétant par des .zéros à gauche, si nécessaire, l'une des deux chaînes pour qu'elles soient de même longueur. CA et CD seront Formées chacune de n chiffres ci auront la forme suivante :
CA = "AN...A4A3A2A1"
CD = "BN .. B4B3B2B1"
c) Générer une matrice carrée M de taille nxn, tel que :
M[i][j] = te produit du ième chiffre de la chaîne CA par le jème chiffre de la chaîne CH
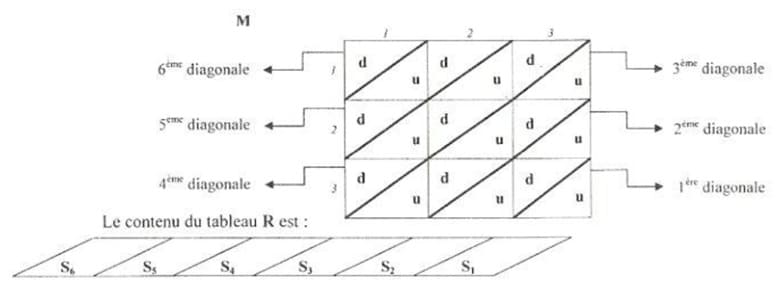
d) La matrice M est supposée formée par 2xri diagonales en plaçant le chiffre des dizaines dans la moitié supérieure Lie chaque case et le chiffre des unités dans b moitié inférieure de la même case, comme le montre la figure ci-après pour le cas où n=3.
Remplir chacune des cases d'un tableau R de taille lin par la somme des chiffres d'une diagonale de la matrice PA en commençant par la diagonale du coin inférieur droit jusqu'à celle du coin supérieur gauche.
Avec :
- d et u sont respectivement. le chiffre des dizaines et le chiffre des unités de chaque élément de la matrice.
- Si est la somme des chiffres de la diagonale leI ,
e) En commençant par la dernière case du tableau R et pour chaque élément R[i] supérieur ou égal à 10, mettre à jour son contenu comme suit :
R[i-1] = R[i-1] + R[i] Div 10
R[i] = R[i] Div 10
f) Le résultat du produit des deux entiers A et B est obtenu en concaténant rJLL2anche i clroillo les éléments du tableau R obtenus dans l'étape précédente.
Exemple Pour A = 7842 et B = 35
a) Les deux chaînes CA et CH seront respectivement "7842" et "35".
b) Après ajustement des longueurs des deux chaînes, on aura : CA="7842", CF="0035" et n =4.

Travail demandé :
1- Analyser le problème en le décomposant en modules ( prévoir la saisie des entiers. A et B (avec A et B flans [10, 10.000] et l'affichage du résultat. )
2- Ecrire les algorithmes des modules envisages.
Solution Algorithmique
Dans cet algorithme, On va utiliser deux fonctions et six procédures:
- la fonction saisie()
- la procédure convert_chaine()
- la procédure remplir_matrice()
- la procédure afficher_matrice()
- la procédure remplir_tableau()
- la procédure maj_tableau()
- la procédure afficher_tableau()
- la fonction resultat()
Algorithme du programme Principal
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
Algorithme multiplication Debut # Saisie de deux entiers a <- saisie(10, 10000) b <- saisie(10, 10000) # Conversion en chaînes de caractères ca <- Convch(a) cb <- Convch(b) # Mise à la même longueur des deux chaînes convert_chaine() # Remplissage et affichage de la matrice des produits remplir_matrice(m, long(ca), ca, cb) Ecrire ('*** Matrice M ***') afficher_matrice(m, long(ca)) # Remplissage et affichage du tableau des diagonales remplir_tableau(m, long(ca), r) Ecrire('*** Tableau R ***') afficher_tableau(r, 2 * long(ca)) # Mise à jour du tableau (gestion des retenues) maj_tableau(r, 2 * long(ca)) Ecrire('\n*** Tableau R apres MAJ ***') afficher_tableau(r, 2 * long(ca)) # Affichage du résultat final de la multiplication Ecrire('\n*** Resultat de la multiplication ***') Ecrire(resultat(r, 2 * long(ca))) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| a | entier |
| b | entier |
| ca | chaîne |
| cb | chaîne |
| m | matrice |
| r | tableau |
La fonction saisie
Cette fonction permet de saisir un entier valide compris entre deux bornes inf et sup.
1- Elle demande à l’utilisateur de saisir un entier n.
2- Elle vérifie que n appartient à l’intervalle [𝑖𝑛𝑓,𝑠𝑢𝑝]
3- Si la valeur saisie n’est pas valide, la fonction redemande la saisie jusqu’à obtenir un entier correct.
4- Elle retourne finalement la valeur valide saisie par l’utilisateur.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
Fonction saisie():entier # Saisie initiale Ecrire('donner n tel que ' ,inf , '<= n <= ' , sup, ': ') Lire(n) # Répéter la saisie tant que n n'est pas valide Tant que Non(inf <= n <= sup) faire Ecrire('donner n tel que ' ,inf , '<= n <= ' , sup, ': ') Lire(n) Fin tant que # Retourner la valeur correcte retourner n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La procédure convert_chaine
Cette procédure sert à rendre les deux chaînes de caractères ca et cb de même longueur en ajoutant des zéros à gauche de la chaîne la plus courte.
1- Si ca est plus courte que cb, on ajoute des '0' au début de ca.
2- Si cb est plus courte que ca, on ajoute des '0' au début de cb.
3- À la fin de l’exécution, ca et cb ont exactement la même longueur.
|
1 2 3 4 5 6 7 8 9 10 |
Procedure convert_chaine(): # Ajouter des zéros à gauche de ca si elle est plus courte Tant que long(ca) < long(cb) faire ca <- '0' + ca Fin tant que # Ajouter des zéros à gauche de cb si elle est plus courte Tant que long(ca) > long(cb) faire cb <- '0' + cb Fin tant que Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| ca | chaîne (variable globale) |
| cb | chaîne (variable globale) |
La procédure remplir_matrice
Cette procédure permet de trier un tableau t par ordre croissant en utilisant l’algorithme du tri rapide (Quick Sort).
1- Elle choisit un pivot (l’élément du milieu du sous-tableau).
2- Elle place ce pivot au début du sous-tableau.
3- Elle partitionne le tableau :
- Tous les éléments inférieurs au pivot sont déplacés à gauche.
- Les éléments supérieurs ou égaux restent à droite.
- Elle remet ensuite le pivot à sa position définitive dans le tableau.
4- Elle applique récursivement le même traitement au sous-tableau situé à gauche du pivot, puis au sous-tableau situé à droite du pivot
|
1 2 3 4 5 6 7 |
Procédure remplir_matrice(m:matrice, n:entier, ca:chaîne, cb:chaîne) Pour i de 0 à n-1 faire Pour j de 0 à n-1 faire m[i][j] <- Valeur(ca[i]) * Valeur(cb[j]) Fin pour Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| j | entier |
La procédure afficher_matrice
Cette procédure affiche à l’écran les éléments de la matrice de caractères ligne par ligne.
1- Elle parcourt la matrice selon le nombre de lignes l et de colonnes c.
2- Elle affiche chaque caractère de la matrice avec un espace entre les éléments.
3- Elle passe à la ligne après l’affichage de chaque ligne de la matrice.
|
1 2 3 4 5 6 7 8 9 |
Procedure afficher_matrice(m:matrice, n:entier) Ecrire('*** Contenu de la matrice M ***') Pour i de 0 à n-1 faire Pour j de 0 à n-1 faire Ecrire(m[i][j], ' ') Fin pour Ecrire() Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| j | entier |
La procédure remplir_tableau
Cette procédure permet de remplir le tableau r en additionnant les chiffres des éléments de la matrice m diagonale par diagonale.
1- Elle parcourt toutes les diagonales de la matrice carrée m de taille n × n.
2- Pour chaque élément m[i][j] appartenant à une diagonale :
3- Elle transforme sa valeur en chaîne de caractères.
4- Elle force l’écriture sur deux chiffres (en ajoutant un zéro à gauche si nécessaire).
6- Elle additionne séparément les deux chiffres : le chiffre des dizaines est ajouté à r[k] et le chiffre des unités est ajouté à r[k+1].
7- Le tableau r contient ainsi les sommes partielles des produits, organisées selon les diagonales.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
Procédure remplir_tableau(m:matrice, n:entier, r:tableau) Pour k de 0 à 2*n-1 faire # Indice des diagonales Pour i de 0 à n-1 j <- k - i # Calcul de la colonne Si 0 <= j < n alors ch <- Convch(m[i][j]) # Conversion en chaîne Si long(ch) = 1 alors # Assurer deux chiffres ch <- '0' + ch Fin si # Addition des chiffres séparément r[k] <- r[k] + Valeur(ch[0]) r[k + 1] <- r[k + 1] + Valeur(ch[1]) Fin si Fin pour Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| j | entier |
| k | entier |
La procédure maj_tableau
Cette procédure permet de mettre à jour le tableau r en gérant les retenues en base 10, exactement comme dans une addition ou une multiplication manuelle.
Elle parcourt le tableau r de l’indice 1 jusqu’à n-1.
Pour chaque case r[i] : Elle transfère la retenue (r[i] div 10) vers la case précédente r[i-1].
Elle conserve uniquement le chiffre des unités dans r[i] grâce à l’opération modulo 10.
À la fin, chaque case de r contient un seul chiffre compris entre 0 et 9.
|
1 2 3 4 5 6 |
Procedure maj_tableau(r:tableau, n:entier) Pour i de 1 à n-1 faire r[i - 1] <- r[i - 1] + r[i] div 10 r[i] = r[i] mod 10 Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
La procédure afficher_tableau
Cette procédure permet d’afficher les n premiers éléments du tableau t sur une seule ligne.
1- Elle parcourt le tableau t de l’indice 0 à n-1.
2- Elle affiche chaque élément suivi d’un espace, sans passer à la ligne après chaque affichage.
|
1 2 3 4 5 |
Procedure afficher_tableau(t:tableau, n:entier) Pour i de 0 à n-1 faire Ecrire(t[i]) Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
La fonction resultat
Cette fonction permet de transformer les n premiers éléments du tableau t en une chaîne de caractères représentant le résultat final du calcul (produit).
1- Elle parcourt le tableau t de l’indice 0 à n-1.
2- Elle concatène chaque élément du tableau à une chaîne liste.
3- Elle retourne la chaîne obtenue, qui correspond au nombre final calculé.
|
1 2 3 4 5 6 7 |
Fonction resultat(t:tableau, n:entier):chaine liste <- '' Pour i de 0 à n-1 faire liste <- liste + Convch(t[i]) Fin pour retourner liste Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 |
from numpy import * # -------------------------------------------------- # Définition des dimensions maximales de la matrice # -------------------------------------------------- lignes = 100 # Nombre maximal de lignes de la matrice colonnes = 100 # Nombre maximal de colonnes de la matrice # -------------------------------------------------- # Création d'une matrice m de taille 100x100 # Initialisée à 0 # Cette matrice servira à stocker les produits # des chiffres de deux nombres # -------------------------------------------------- m = array([[int()] * colonnes] * lignes) # -------------------------------------------------- # Création d'un tableau r de taille 100 # Il servira à stocker les sommes des diagonales # -------------------------------------------------- r = array([int()] * 100) # -------------------------------------------------- # Fonction de saisie sécurisée d'un entier # Elle force l'utilisateur à saisir un nombre # compris entre inf et sup # -------------------------------------------------- def saisie(inf, sup): # Saisie initiale n = int(input('donner n tel que ' + str(inf) + '<= n <= ' + str(sup) + ': ')) # Répéter la saisie tant que n n'est pas valide while not (inf <= n <= sup): n = int(input('donner n tel que ' + str(inf) + '<= n <= ' + str(sup) + ': ')) # Retourner la valeur correcte return n # -------------------------------------------------- # Procédure qui rend les deux chaînes ca et cb # de même longueur en ajoutant des zéros à gauche # -------------------------------------------------- def convert_chaine(): global ca, cb # Ajouter des zéros à gauche de ca si elle est plus courte while len(ca) < len(cb): ca = '0' + ca # Ajouter des zéros à gauche de cb si elle est plus courte while len(ca) > len(cb): cb = '0' + cb # -------------------------------------------------- # Procédure qui remplit la matrice m # Chaque élément m[i][j] contient le produit # du chiffre ca[i] par le chiffre cb[j] # -------------------------------------------------- def remplir_matrice(m, n, ca, cb): for i in range(n): for j in range(n): m[i][j] = int(ca[i]) * int(cb[j]) # -------------------------------------------------- # Procédure d'affichage de la matrice m # -------------------------------------------------- def afficher_matrice(m, n): for i in range(n): for j in range(n): print(m[i][j], end=' ') print() # -------------------------------------------------- # Procédure qui remplit le tableau r # en parcourant les diagonales de la matrice # -------------------------------------------------- def remplir_tableau(m, n, r): for k in range(2 * n - 1): # Indice des diagonales for i in range(n): j = k - i # Calcul de la colonne if 0 <= j < n: ch = str(m[i][j]) # Conversion en chaîne if len(ch) == 1: # Assurer deux chiffres ch = '0' + ch # Addition des chiffres séparément r[k] = r[k] + int(ch[0]) r[k + 1] = r[k + 1] + int(ch[1]) # -------------------------------------------------- # Procédure de mise à jour du tableau r # Gestion des retenues (base 10) # -------------------------------------------------- def maj_tableau(r, n): for i in range(1, n): r[i - 1] = r[i - 1] + r[i] // 10 r[i] = r[i] % 10 # -------------------------------------------------- # Procédure d'affichage d'un tableau # -------------------------------------------------- def afficher_tableau(t, n): for i in range(n): print(t[i], end=' ') # -------------------------------------------------- # Fonction qui transforme le tableau résultat # en une chaîne représentant le produit final # -------------------------------------------------- def resultat(t, n): liste = '' for i in range(n): liste = liste + str(t[i]) return liste # ===================== Programme principal ===================== # Saisie de deux entiers a = saisie(10, 10000) b = saisie(10, 10000) # Conversion en chaînes de caractères ca = str(a) cb = str(b) # Mise à la même longueur des deux chaînes convert_chaine() # Remplissage et affichage de la matrice des produits remplir_matrice(m, len(ca), ca, cb) print('*** Matrice M ***') afficher_matrice(m, len(ca)) # Remplissage et affichage du tableau des diagonales remplir_tableau(m, len(ca), r) print('*** Tableau R ***') afficher_tableau(r, 2 * len(ca)) # Mise à jour du tableau (gestion des retenues) maj_tableau(r, 2 * len(ca)) print('\n*** Tableau R apres MAJ ***') afficher_tableau(r, 2 * len(ca)) # Affichage du résultat final de la multiplication print('\n*** Resultat de la multiplication ***') print(resultat(r, 2 * len(ca))) |
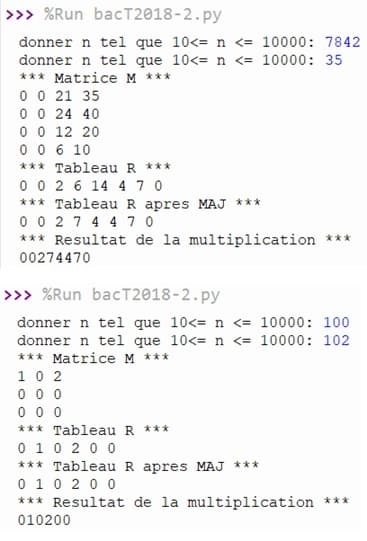
Exécution du programme
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés