Jeu Dominos – Bac théorique – Section informatique – 2021

Sujet (Algo et programmation - Bac 2021)
Le jeu de dominos est un jeu chinois qui comporte 28 dominos. Un domino est formé de 2 parties. Chaque partie contient de 0 à 6 points.
Une suite de dominos est dite valide lorsque la 2ëmepartie d'un domino est identique à la l partie du domino voisin.

La suite de dominos de la Figure 2 est invalide car la 2' partie du 2éne domino (6 points) est différente de la l ere partie du domino voisin (2 points).
Afin d'automatiser ce jeu, on se propose d'utiliser un tableau D d'entiers. Chaque case contient une valeur comprise entre 0 et 6. Ainsi, le tableau correspondant à la Figure 1 est représenté comme suit :
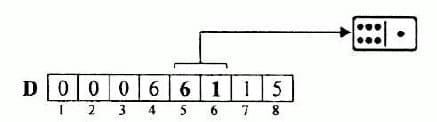
Les paires (D111, D121), (D[3], D141), (Di5j, D[6]) et (Dr], D[81) représentent une suite de 4 dominos.
Travail demandé
1. Analyser le problème en le décomposant en modules.
2. Ecrire les algorithmes des modules envisagés.
Solution Algorithmique
Dans cet algorithme, On va utiliser trois fonctions et cinq procédures:
- la fonction saisie()
- la fonction saisie_domino()
- la procédure remplir_tableau()
- la fonction verifier_suite_dominos()
Algorithme du programme Principal
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
Algorithme cryptage Debut # Saisie du taille du tableau d n <- saisie() # Remplissage du tableau avec les valeurs saisies remplir_tableau(d, n) # Vérification et affichage du résultat Si verifier_suite_dominos(d, n) alors Ecrire('Suite dominos valide') Sinon Ecrire('Suite dominos non valide') Fin si Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
| d | tableau |
La fonction saisie()
La fonction saisie permet à l’utilisateur de saisir un nombre entier pair compris entre 4 et 56, en vérifiant sa validité avant de le retourner.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
Fonction saisie(): # Saisie initiale de n Ecrire('donner n pair tel que 4<=n<=56 : ') Lire(n) # Vérification de la validité de la saisie # n doit être pair et compris entre 4 et 56 Tant que Non(4 <= n <= 56) ou n % 2 != 0 faire Ecrire('donner n pair tel que 4<=n<=56 : ') Lire(n) Fin tant que # Retourner la valeur valide return n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La fonction saisie_domino()
La fonction saisie permet à l’utilisateur de saisir un nombre entier pair compris entre 4 et 56, en vérifiant sa validité avant de le retourner.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
Fonction saisie(): # Saisie initiale de n Ecrire('donner n tel que 0<=n<=6: ') Lire(n) # Vérification de la validité de la saisie # n doit être pair et compris entre 4 et 56 Tant que Non(0<=n<=6) faire Ecrire('donner n tel que 0<=n<=6: ') Lire(n) Fin tant que # Retourner la valeur valide retourner n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La procédure remplir_tableau
Le rôle de la procédure remplir_tableau est de remplir le tableau t avec n valeurs de dominos saisies par l’utilisateur.
|
1 2 3 4 5 |
Procédure remplir_tableau(t:tableau;n:entier) Pour i de 0 à n-1 faire t[i] <- saisie_domino() Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
La procédure afficher_tableau
Cette procédure affiche à l’écran les n premiers enregistrements du tableau t.
|
1 2 3 4 5 |
Procédure afficher_tableau(t:tableau;n:entier): Pour i de 0 à n-1 faire Ecrire(t[i]) Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
La fonction verifier_suite_dominos
La fonction verifier_suite_dominos vérifie si la suite de dominos stockée dans le tableau t est valide, c’est-à-dire que chaque paire de dominos consécutifs contient deux valeurs identiques.
|
1 2 3 4 5 6 7 8 9 |
Fonction verifier_suite_dominos(t:tableau, n:entier):booleen i <- 1 # Parcours des paires de dominos Tant que (i < n - 3) et (t[i] = t[i + 1]) faire i <- i + 2 Fin tant que # Retourne True si la dernière paire est valide retourner (t[i] = t[i + 1]) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 |
from numpy import * # -------------------------------------------------- # Création d'un tableau d'entiers de taille 100 # destiné à stocker les valeurs des dominos # -------------------------------------------------- d = array([int()] * 100) # -------------------------------------------------- # Fonction qui permet de saisir un nombre pair n # tel que 4 ≤ n ≤ 56 # -------------------------------------------------- def saisie(): # Saisie initiale de n n = int(input('donner n pair tel que 4<=n<=56 : ')) # Vérification de la validité de la saisie # n doit être pair et compris entre 4 et 56 while not (4 <= n <= 56) or n % 2 != 0: n = int(input('donner n paire tel que 4<=n<=56 : ')) # Retourner la valeur valide return n # -------------------------------------------------- # Fonction qui permet de saisir une valeur de domino # comprise entre 0 et 6 # -------------------------------------------------- def saisie_domino(): # Saisie initiale n = int(input('donner n tel que 0<=n<=6 : ')) # Vérification de la validité de la saisie while not (0 <= n <= 6): n = int(input('donner n tel que 0<=n<=6 : ')) # Retourner la valeur valide return n # -------------------------------------------------- # Procédure qui remplit le tableau t avec n valeurs # de dominos saisies par l'utilisateur # -------------------------------------------------- def remplir_tableau(t, n): for i in range(n): t[i] = saisie_domino() # -------------------------------------------------- # Fonction qui vérifie si la suite de dominos est valide # Chaque paire de dominos doit être composée de deux # valeurs identiques consécutives # -------------------------------------------------- def verifier_suite_dominos(t, n): i = 1 # Parcours des paires de dominos while (i < n - 3) and (t[i] == t[i + 1]): i = i + 2 # Retourne True si la dernière paire est valide return (t[i] == t[i + 1]) # -------------------------------------------------- # Programme principal # -------------------------------------------------- # Saisie du nombre total de dominos n = saisie() # Remplissage du tableau avec les valeurs saisies remplir_tableau(d, n) # Vérification et affichage du résultat if verifier_suite_dominos(d, n): print('Suite dominos valide') else: print('Suite dominos non valide') |
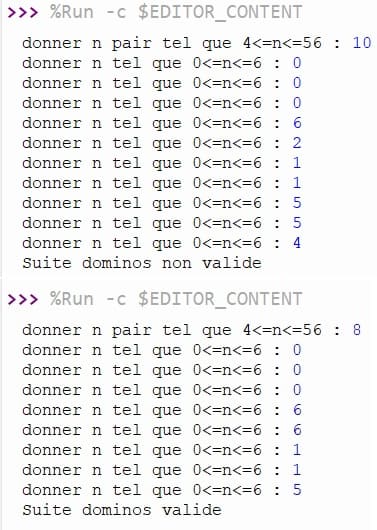
Exécution du programme
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés