Conversion entier – Bac théorique – Section informatique – 2022

Sujet (Algo et programmation - Bac 2022)
On se propose de réaliser la conversion d’un entier naturel strictement positif N dans une base B donnée (avec 2 ≤ B ≤ 16).
Pour cela on effectue des divisions euclidiennes par B, les restes successifs seront rangés dans un tableau Restes à Rmax éléments (avec Rmax = 15) puis on inverse les éléments du tableau Restes et on les concatène tout en convertissant les valeurs supérieures ou égales à 10 (dans le cas où la base B >10) en leurs équivalents dans la base B.
Travail demandé :
1- Ecrire un algorithme d’une procédure SAISIE(P, Binf, Bsup) qui permet de saisir un entier naturel P tel que Binf ≤ P ≤ Bsup (avec Binf et Bsup deux entiers naturels).
2- Ecrire un algorithme d’une procédure RANGER (N, B, RESTES, NbreR) qui permet de :
- Ranger dans un tableau RESTES les restes successifs de la suite des divisions euclidiennes par B jusqu’à obtenir un quotient égal à 0 (dans la première division euclidienne on divise N par B, puis on divise le quotient obtenu par B, etc.).
- Calculer le nombre des restes NbreR.
3- Ecrire un algorithme d’une procédure RENVERSER(RESTES, NbreR) qui renverse les NbreR éléments rangés dans le tableau RESTES. (Permuter RESTES [0] avec RESTES [NbreR-1], RESTES [1] avec RESTES [NbreR-2], etc.)
4- Ecrire un algorithme d’une fonction CONVERT(C) qui permet de retourner le caractère qui correspond à l’entier C (avec 0 ≤ C ≤ 15).
Exemples : CONVERT (0) retourne le caractère "0", CONVERT (9) retourne le caractère "9", CONVERT (10) retourne le caractère "A", CONVERT (15) retourne le caractère "F"
5- Ecrire un algorithme d’une procédure CONCATENATION(RESTES, NbreR) qui, en utilisant la fonction CONVERT et la procédure RENVERSER, affiche l’équivalent du nombre N dans la base B en concaténant les éléments du tableau RESTES.
6- En faisant appel uniquement aux modules déjà définis, écrire un algorithme d’un programme principal intitulé CONVERSION qui permet de saisir un entier naturel N (avec 100 ≤ N ≤ 20000) et une base B (avec 2 ≤ B ≤ 16) et d’afficher le résultat de la conversion du nombre décimal N dans la base B.

Solution Algorithmique
Dans cet algorithme, On va utiliser deux fonctions et quatre procédures :
- la fonction saisie()
- la procédure remplir_tableau()
- la procédure inverser_tableau()
- la procédure afficher_tableau()
- la fonction convert()
- la procédure concatenation()
Algorithme du programme Principal
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Algorithme conversion_entier Debut # Variable globale qui représente la taille réelle # du tableau "reste" utilisée taille <- 0 # Saisie du nombre à convertir (entre 100 et 20000) p <- saisie(100, 20000) # Saisie de la base de conversion (entre 2 et 16) b <- saisie(2, 16) # Remplissage du tableau avec les restes remplir_tableau(reste, p, b) Ecrire('*** contenu du tableau reste ***') afficher_tableau(reste, taille) # Inversion du tableau pour obtenir l'ordre correct inverser_tableau(reste, taille) Ecrire('*** contenu du tableau reste inverse ***') afficher_tableau(reste, taille) # Affichage du résultat final de la conversion concatenation(reste, taille) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| p | entier |
| b | matrice |
| reste | tableau |
| taille | entier |
La fonction saisie
La fonction saisie(Binf, Bsup) permet de saisir un entier compris entre deux bornes données, en garantissant que la valeur entrée par l’utilisateur est valide.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
Fonction saisie(Binf,Bsup):entier # Saisie initiale Ecrire('donner n tq ' + str(Binf) + '<=p<=' + str(Bsup) + ': ') Lire(p) # Vérification de la validité de la saisie Tant que Non (Binf <= p <= Bsup) faire Ecrire('donner n tq ' + str(Binf) + '<=p<=' + str(Bsup) + ': ') Lire(p) Fin tant que # Retourner la valeur valide retourner p Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| p | entier |
La procédure remplir_tableau
Cette procédure permet de convertir un nombre décimal p en une base b en stockant les restes successifs de la division de p par b dans le tableau reste.
|
1 2 3 4 5 6 7 8 |
Procedure remplir_tableau(reste:tableau, p:entier, b:entier) Tant que p != 0 faire r <- p mod b # Calcul du reste reste[taille] <- r # Stockage du reste dans le tableau p <- p div b # Division entière de p par b taille <- taille + 1 Fin tant que Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| r | entier |
| taille | entier (variable globale) |
La procédure inverser_tableau
Cette procédure permet d’inverser l’ordre des n premiers éléments du tableau t.
|
1 2 3 4 5 6 7 |
Procedure inverser_tableau(t:tableau, n:entier) Pour i de 0 à (n div 2 -1) faire temp <- t[i] t[i] <- t[n-1-i] t[n-1-i] <- temp Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| temp | entier |
La procédure afficher_tableau
Cette procédure permet d’afficher les n premiers éléments du tableau t sur une seule ligne, séparés par des espaces.
|
1 2 3 4 5 6 |
Procedure afficher_tableau(t:tableau, n:entier) Pour i de 0 à n-1 faire Ecrire(t[i],' ') Fin pour Ecrire() Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
La fonction convert
Cette fonction permet de convertir un chiffre numérique en son caractère correspondant lors d’une conversion en base comprise entre 2 et 16.
|
1 2 3 4 5 6 7 |
Fonction convert(nbr:entier):chaine Si 0 <= nbr <= 9 alors retourner Convch(nbr) Sinon Si 10 <= nbr <= 15 alors retourner chr(nbr + 55) # 10 -> 'A', 11 -> 'B', ... Fin si Fin |
La procédure concatenation
Cette procédure concatène les n premiers éléments du tableau t après conversion en caractères, afin d’afficher le nombre final en base b.
|
1 2 3 4 5 6 7 |
Procedure concatenation(t:tableau, n:entier) resultat <- '' Pour i de 0 à n-1 faire resultat <- resultat + convert(t[i]) Fin pour Ecrire('le resultat de la conversion est ', resultat) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| resultat | chaîne |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 |
from numpy import * # -------------------------------------------------- # Déclaration d'un tableau de taille maximale 50 # qui contiendra les restes de la division # -------------------------------------------------- reste = array([int()] * 50) # -------------------------------------------------- # Fonction de saisie sécurisée # Elle permet de saisir un entier p tel que # Binf <= p <= Bsup # -------------------------------------------------- def saisie(Binf, Bsup): # Saisie initiale p = int(input('donner n tq ' + str(Binf) + '<=p<=' + str(Bsup) + ': ')) # Vérification de la validité de la saisie while not (Binf <= p <= Bsup): p = int(input('donner n tq ' + str(Binf) + '<=p<=' + str(Bsup) + ': ')) # Retourner la valeur valide return p # -------------------------------------------------- # Procédure qui remplit le tableau "reste" # avec les restes successifs de la division de p par b # (conversion de p en base b) # -------------------------------------------------- def remplir_tableau(reste, p, b): global taille # Utilisation de la variable globale "taille" while p != 0: r = p % b # Calcul du reste reste[taille] = r # Stockage du reste dans le tableau p = p // b # Division entière de p par b taille = taille + 1 # -------------------------------------------------- # Procédure qui inverse les n premiers éléments # du tableau t # -------------------------------------------------- def inverser_tableau(t, n): for i in range(n // 2): temp = t[i] t[i] = t[n - 1 - i] t[n - 1 - i] = temp # -------------------------------------------------- # Procédure qui affiche les n premiers éléments # du tableau t # -------------------------------------------------- def afficher_tableau(t, n): for i in range(n): print(t[i], end=' ') print() # -------------------------------------------------- # Fonction qui convertit un chiffre en caractère # (0–9 -> '0' à '9', 10–15 -> 'A' à 'F') # -------------------------------------------------- def convert(nbr): if 0 <= nbr <= 9: return str(nbr) elif 10 <= nbr <= 15: return chr(nbr + 55) # 10 -> 'A', 11 -> 'B', ... # -------------------------------------------------- # Procédure qui concatène les chiffres convertis # du tableau t pour former le nombre final # -------------------------------------------------- def concatenation(t, n): resultat = '' for i in range(n): resultat = resultat + convert(t[i]) print('le resultat de la conversion est ', resultat) # -------------------------------------------------- # Programme principal # -------------------------------------------------- # Variable globale qui représente la taille réelle # du tableau "reste" utilisée taille = 0 # Saisie du nombre à convertir (entre 100 et 20000) p = saisie(100, 20000) # Saisie de la base de conversion (entre 2 et 16) b = saisie(2, 16) # Remplissage du tableau avec les restes remplir_tableau(reste, p, b) print('*** contenu du tableau reste ***') afficher_tableau(reste, taille) # Inversion du tableau pour obtenir l'ordre correct inverser_tableau(reste, taille) print('*** contenu du tableau reste inverse ***') afficher_tableau(reste, taille) # Affichage du résultat final de la conversion concatenation(reste, taille) |
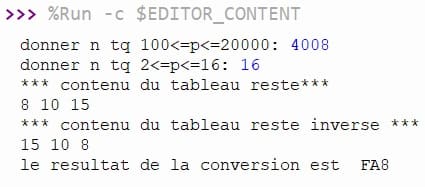
Exécution du programme
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés
























