Nombre de Keith – Bac théorique – Section informatique – 2025
Sujet (Algo et programmation - Bac 2025)
Soit K un entier de d chiffres (avec d >= 2) ayant la forme C1C2 … Cd. A partir de ce nombre on définit une suite U telle que les d premiers termes sont les d chiffres du nombre K. Ensuite chaque terme suivant est calculé en additionnant les d termes précédents.
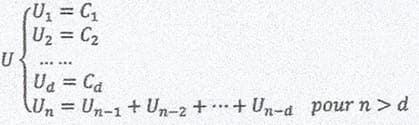
Le nombre K est appelé nombre de Keith, si à un moment donné, un terme de la suite U est égal au nombre K.
Exemples :
- Pour K = 197, le nombre de chiffres qui le forment est égal à 3, donc d = 3 et la suite U est définie par :
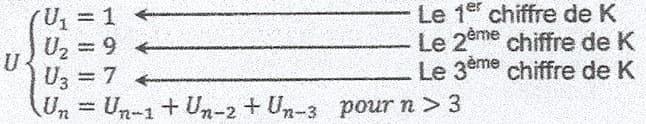
Les termes de la suite sont : U1=1, U2=9, U3=7, U4=17, U5=33, U6=57, U7=107, U8=197, ... U8 = 197 = K, K est un terme de la suite donc K est un nombre de Keith.
- Pour k = 24, le nombre de chiffres qui le forment est égal à 2, donc d = 2 et la suite U est définie par :
Les termes de la suite sont U1=2, U2=4, U3=6, U4=10, U5=16, U6=26, ... . Comme U6=26>K donc K n'est pas un terme de la suite et par conséquent K n'est pas un nombre de Keith.
Travail demandé :
1) Ecrire un algorithme d'une fonction Verif(K) qui permet de retourner
- La valeur de n telle que Un=k, si K est un nombre de Keith
- La valeur -1 dans le cas contraire.
Exemples : Verif(197) retourne 8 et Verif(24) retourne -1
2) En utilisant la fonction Verif, écrire un algorithme d'un programme qui permet de remplir un tableau d'enregistrements NK par les nombres de Keith qui sont inférieurs à 100000, sachant que chaque enregistrement du tableau NK contient les champs suivants :
- Nbre : le nombre de Keith.
- Num : le numéro du terme de la suite U qui est égal au nombre de Keith contenu dans le champ Nbre.
Solution Algorithmique
Dans cet algorithme, On va utiliser deux fonctions et deux procédures :
- la fonction saisie()
- la fonction verif()
- la procédure remplir_nk()
- la procédure afficher_nk()
Algorithme du programme Principal
|
1 2 3 4 5 6 7 8 9 10 |
Algorithme nombre_keith Debut # Initialisation de la taille logique du tableau taille <- 0 # Remplissage du tableau d’enregistrements remplir_nk(t) # Affichage du contenu Ecrire('*** Contenu du tableau d enregistrement ***') afficher_nk(t, taille) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| taille | entier |
| t | tableau des enregistrements |
La fonction saisie
Cette fonction permet de saisir et retourner un entier >= 10 en contrôlant la validité de la saisie.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
Fonction saisie():entier # Demande à l'utilisateur de saisir un entier n >= 10 Ecrire('donner un entier >= 10: ')) Lire(n) # Vérification de la validité de la saisie Tant que Non (n >= 10) faire Ecrire('donner un entier >= 10: ')) Lire(n) Fin tant que # Retourne la valeur valide saisie par l'utilisateur retourner n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La fonction verif
La fonction verif(k) permet de vérifier si un entier k peut être obtenu comme terme d’une suite numérique construite à partir des chiffres de k, selon la règle de Keith calcul donnée.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
Fonction verif(k:entier):booleen # Initialisation du tableau u à 0 Pour i de 0 à 999 faire u[i] <- 0 Fin pour # Transformation de k en chaîne de caractères ch <- Convch(k) d <- long(ch) # Remplissage des premières cases de u # avec les chiffres de k Pour i de 0 à d-1 faire u[i+1] <- Valeur(ch[i]) Fin pour # n représente l’indice courant n <- d # Calcul progressif des valeurs de u Tant que u[n]<k faire Pour i de n-long(ch)+1 à n faire u[n+1] <- u[n+1] + u[i] Fin pour n <- n+1 # Si la valeur obtenue est égale à k Si u[n] = k: alors retourner n # retourner le rang Sinon retourner -1 # k non vérifié Fin si Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| u | tableau |
| ch | chaîne |
| d | entier |
| n | entier |
La procédure remplir_nk
La procédure remplir_nk permet de remplir le tableau d’enregistrements t par tous les entiers compris entre 10 et 999 qui vérifient la règle de Keith donnée par la fonction verif.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
Procédure remplir_nk(t:tableau) # Parcours des nombres de 10 à 999 Pour i de 10 à 999 faire # Vérifier si le nombre satisfait la condition Si verif(i) != -1 alors # Création d’un enregistrement nk nk = enregistrement( nbre = Entier(), # nombre num = Entier() # rang ) # Remplissage de l’enregistrement nk['nbre'] <- i nk['num'] <- verif(i) # Insertion dans le tableau t t[taille] <- nk taille <- taille+1 Fin Si Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| nk | enregistrement |
| taille | entier (variable globale) |
La procédure afficher_nk
La procédure affiche le contenu du tableau d'enregistrement t.
|
1 2 3 4 5 |
Procédure afficher_nk(t:tableau, taille:entier) Pour i de 0 à taille -1 faire Ecrire(t[i]) Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 |
from numpy import * # -------------------------------------------------- # Déclaration des tableaux globaux # -------------------------------------------------- # Tableau u : tableau d'entiers de taille 1000 # Il servira à stocker des valeurs intermédiaires u = array([int()] * 1000) # Tableau t : tableau d'enregistrements # Chaque élément contiendra un nombre et son rang t = array([{}] * 1000) # -------------------------------------------------- # Fonction de saisie sécurisée # Elle demande un entier >= 10 # -------------------------------------------------- def saisie(): # Première saisie n = int(input('donner un entier >= 10')) # Répéter la saisie tant que la valeur n'est pas valide while not (n >= 10): n = int(input('donner un entier >= 10')) # Retourner la valeur valide return n # -------------------------------------------------- # Fonction de vérification # Elle vérifie si k peut être obtenu # selon une règle de calcul donnée # -------------------------------------------------- def verif(k): # Initialisation du tableau u à 0 for i in range(1000): u[i] = 0 # Transformation de k en chaîne de caractères ch = str(k) d = len(ch) # Remplissage des premières cases de u # avec les chiffres de k for i in range(d): u[i + 1] = int(ch[i]) # n représente l’indice courant n = d # Calcul progressif des valeurs de u while u[n] < k: for i in range(n - len(ch) + 1, n + 1): u[n + 1] = u[n + 1] + u[i] n = n + 1 # Si la valeur obtenue est égale à k if u[n] == k: return n # retourner le rang else: return -1 # k non vérifié # -------------------------------------------------- # Procédure de remplissage du tableau t # -------------------------------------------------- def remplir_nk(t): global taille # Parcours des nombres de 10 à 999 for i in range(10, 1000): # Vérifier si le nombre satisfait la condition if verif(i) != -1: # Création d’un enregistrement nk nk = dict( nbre = int(), # nombre num = int() # rang ) # Remplissage de l’enregistrement nk['nbre'] = i nk['num'] = verif(i) # Insertion dans le tableau t t[taille] = nk taille = taille + 1 # -------------------------------------------------- # Procédure d’affichage du tableau t # -------------------------------------------------- def afficher_nk(t, taille): for i in range(taille): print(t[i]) # -------------------------------------------------- # Programme principal # -------------------------------------------------- # Initialisation de la taille logique du tableau taille = 0 # Remplissage du tableau d’enregistrements remplir_nk(t) # Affichage du contenu print('*** Contenu du tableau d enregistrement ***') afficher_nk(t, taille) |
Exécution du programme
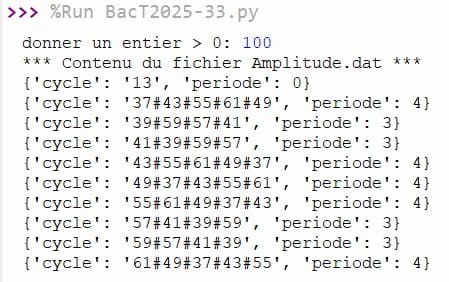
0 commentaire
laisser un commentaire
Passion de robotique
Tutoriels récents
Atelier robotique
Tutoriels populaires
Construction des robots
Tutoriels plus commentés
Bras robotique
Categories
Maison intelligente
