Sujet Matrice – Bac théorique – Section informatique – 2025

Sujet (Algo et programmation - Bac 2025)
Une matrice carrée M1 de taille d*d est dite Matrice multiple d'un premier si le plus grand commun diviseur (PGCD) de ses éléments est un nombre premier.
Pour calculer le PGCD des éléments de la matrice M1, on suit les étapes suivantes
Etape 1 : Stocker tous les éléments de la matrice M1 dans la première ligne d'une matrice M2 de taille d2* d2.
Etape 2 : Remplir les autres lignes de la matrice M2 comme suit : M2[L,C] = PGCD(M2[L-1,C], M2[L-1,C+1]) ,
Dans ce cas, le PGCD des éléments de M1 est le contenu de la case M2[d2 -1,0]
Exemple : Pour d = 2 et la matrice M1 suivante :
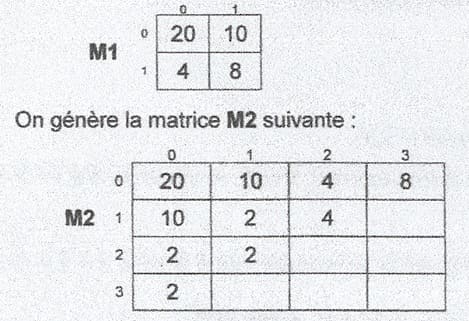
En effet :
- On remplit la ligne d'indice 0 par les éléments de
- On remplit les autres lignes comme suit : La ligne d'indice 1
M2[1,0] = PGCD(20,10) = 10
M2[1,1] = PGCD(10,4) = 2
M2[1,21 = PGCD(4,8) = 4
La ligne d'indice 2 :
M2[2,0] = PGCD(10,2) = 2
M2[2,1]= PGCD(2,4) = 2
La ligne d'indice 3 :
M2[3,0] = PGCD(2,2) = 2
Le PGCD des éléments de Mi est égal â M2[3,0] qui est égal à 2. Comme 2 est un nombre premier, donc Mi est dite Matrice multiple d'un premier.
Travail demandé
1) Écrire un algorithme d'une fonction PGCD(a, b) qui permet de calculer le P000 de deux entiers a et
2) En appliquant les étapes définies précédemment et en utilisant la fonction PGCD de la question 1), écrire un algorithme d'une fonction Verif(M1, d) qui permet de vérifier si la matrice
M1 de taille d*d est dite Matrice multiple d'un premier.
NB:
Ml est de type MAT1
M2 est de type MAT2
Le candidat n'est pas appelé à dresser le tableau de déclaration pour définir les types Mat1 et Mat2
Solution Algorithmique
Dans cet algorithme, On va utiliser trois fonctions et trois procédures :
- la fonction saisie()
- la procédure remplir_matrice_m1()
- la fonction pgcd()
- la procédure remplir_matrice_m2()
- la procédure afficher_matrice()
- la fonction test_premier()
Algorithme du programme Principal
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
Algorithme matrice_premier Debut d <- saisie() # Saisie de la dimension remplir_matrice_m1(m1,d) # Remplissage de la matrice M1 Ecrire("*** Matrice M1 ***") afficher_matrice(m1,d) # Affichage de M1 remplir_matrice_m2(m2,m1,d) # Construction de la matrice M2 Ecrire("*** Matrice M2 ***") afficher_matrice(m2,d*d) # Affichage de M2 # Test si le dernier élément de M2 est un nombre premier Si test_premier(m2[d*d-1,0]) alors Ecrire('M est dite Matrice multiple d un premier') Sinon Ecrire('M est non Matrice multiple d un premier') Fin Si Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| d | entier |
| m1 | Matrice |
| m2 | Matrice |
La fonction saisie
Cette fonction permet de saisir et retourner un entier >= 2 en contrôlant la validité de la saisie.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
Fonction saisie():entier # Demande à l'utilisateur de saisir un entier n >= 2 Ecrire('donner un entier >= 2: ')) Lire(n) # Vérification de la validité de la saisie Tant que Non (n >= 10) faire Ecrire('donner un entier >= 2: ')) Lire(n) Fin tant que # Retourne la valeur valide saisie par l'utilisateur retourner n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La procédure remplir_matrice_m1
Le rôle de la procédure remplir_matrice_m1 est de permettre la saisie et le remplissage des éléments de la matrice m1 de dimension d × d.
|
1 2 3 4 5 6 7 8 9 |
Procédure remplir_matrice_m1(m1:matrice, d:entier) # Remplissage de la matrice m1 de dimension d × d Pour i de 0 à d-1 faire Pour j de 0 à d-1 faire Ecrire('Donner un élément de la matrice M1 : ') Lire(m1[i][j]) Fin pour Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| j | entier |
La fonction pgcd
Le rôle de la fonction pgcd est de calculer et retourner le plus grand commun diviseur (PGCD) de deux entiers a et b en utilisant l’algorithme d’Euclide, qui repose sur des divisions successives jusqu’à ce que le reste devienne nul.
|
1 2 3 4 5 6 7 8 9 |
Fonction pgcd(a:entier, b:entier):entier # Calcul du PGCD de deux entiers a et b # en utilisant l'algorithme d'Euclide Tant que b != 0 faire r <- a mod b # Calcul du reste de la division a <- b # a prend la valeur de b b <- r # b prend la valeur du reste retourner a # a contient le PGCD Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| r | entier |
La procédure remplir_matrice_m2
Le rôle de la procédure remplir_matrice_m2 est de construire la matrice m2 à partir de la matrice m1. Elle commence par placer, dans la première ligne de m2, tous les éléments de m1 mis bout à bout. Ensuite, elle remplit les lignes suivantes de m2 en calculant, pour chaque position, le PGCD de deux éléments voisins de la ligne précédente, jusqu’à obtenir le dernier élément de la matrice.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
Procédure remplir_matrice_m2(m2:matrice, m1:matrice, d:entier) # Remplissage de la première ligne de m2 # avec les éléments de m1 mis bout à bout k <- 0 Pour i de 0 à d-1 faire Pour j de 0 d-1 faire m2[0][k] <- m1[i][j] k <- k+1 Fin pour Fin pour # Construction des lignes suivantes de m2 # chaque élément est le PGCD de deux éléments voisins Pour i de 1 à (d*d)-1 faire Pour j de 1 à (d*d)-1 faire m2[i][j] <- pgcd(m2[i-1][j],m2[i-1][j+1]) Fin pour Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| k | entier |
| i | entier |
| j | entier |
La procédure affihcer_matrice
Le rôle de la procédure remplir_matrice_m1 est de permettre la saisie et le remplissage des éléments de la matrice m1 de dimension d × d.
|
1 2 3 4 5 6 7 8 9 |
Procédure afficher_matrice(m:matrice, d:entier) # Remplissage de la matrice m1 de dimension d × d Pour i de 0 à d-1 faire Pour j de 0 à d-1 faire Ecrire(m[i][j], end=' ') Fin pour Ecrire() Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| j | entier |
La fonction test_premier
Le rôle de la fonction test_premier est de vérifier si un entier n est un nombre premier. Elle teste si n admet un diviseur autre que 1 et lui-même en essayant successivement des diviseurs à partir de 2. La fonction retourne vrai si n est premier et faux dans le cas contraire.
|
1 2 3 4 5 6 7 8 9 10 11 |
Fonction test_premier(n:entier):booleen Si n = 2 alors retourner Faux Sinon i <- 2 Tant que i < n div 2 et n mod i != 0: i <- i + 1 Fin tant que retourner n mod i != 0 Fin si Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 |
from numpy import * # -------------------------------------------------- # Définition des dimensions maximales des matrices # -------------------------------------------------- lignes = 50 # Nombre maximal de lignes colonnes = 50 # Nombre maximal de colonnes # -------------------------------------------------- # Création de deux matrices m1 et m2 de taille maximale # m1 : matrice saisie par l'utilisateur # m2 : matrice utilisée pour stocker les résultats des PGCD # -------------------------------------------------- m1 = array([[int()] * colonnes] * lignes) m2 = array([[int()] * colonnes] * lignes) def saisie(): # Saisie d'un entier n supérieur ou égal à 2 n = int(input('donner un entier >= 2 : ')) # Répéter la saisie tant que n n'est pas valide while not (n >= 2): n = int(input('donner un entier >= 2 : ')) # Retourner la valeur correcte return n def remplir_matrice_m1(m1, d): # Remplissage de la matrice m1 de dimension d × d for i in range(d): for j in range(d): m1[i][j] = int(input('Donner un élément de la matrice M1 : ')) def pgcd(a, b): # Calcul du PGCD de deux entiers a et b # en utilisant l'algorithme d'Euclide while b != 0: r = a % b # Calcul du reste de la division a = b # a prend la valeur de b b = r # b prend la valeur du reste return a # a contient le PGCD def remplir_matrice_m2(m2, m1, d): # Remplissage de la première ligne de m2 # avec les éléments de m1 mis bout à bout k = 0 for i in range(d): for j in range(d): m2[0][k] = m1[i][j] k = k + 1 # Construction des lignes suivantes de m2 # chaque élément est le PGCD de deux éléments voisins for i in range(1, d*d): for j in range(d*d - i): m2[i][j] = pgcd(m2[i-1][j], m2[i-1][j+1]) def afficher_matrice(m, d): # Affichage d'une matrice de dimension d × d for i in range(d): for j in range(d): print(m[i][j], end=' ') print() def test_premier(n): # Vérifie si un nombre n est premier if n == 2: return False else: i = 2 while i < n // i and n % i != 0: i = i + 1 return n % i != 0 # -------------------------------------------------- # Programme principal # -------------------------------------------------- d = saisie() # Saisie de la dimension remplir_matrice_m1(m1, d) # Remplissage de la matrice M1 print("*** Matrice M1 ***") afficher_matrice(m1, d) # Affichage de M1 remplir_matrice_m2(m2, m1, d) # Construction de la matrice M2 print("*** Matrice M2 ***") afficher_matrice(m2, d*d) # Affichage de M2 # Test si le dernier élément de M2 est un nombre premier if test_premier(m2[d*d-1, 0]): print('M est dite Matrice multiple d un premier') else: print('M est non Matrice multiple d un premier') |
Exécution du programme
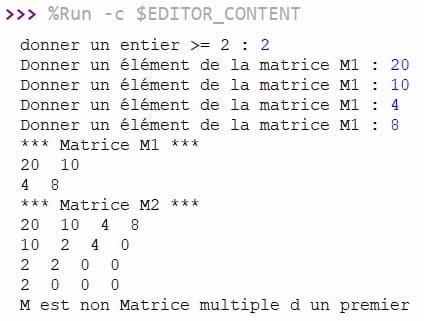
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés




















