Chemins Matrice – Bac théorique – Section informatique – 2009

Sujet (Algo et programmation - Bac 2009)
Soit p et q deux entiers naturels tels que 5 :5_ p < q < 32. On se propose de remplir une matrice M à p lignes et q colonnes par des zéros (0) et des uns (1) de la façon suivante : On mettra 1 dans toute cellule M[i , j] si les représentations de i et de j dans la base 2 ont au moins une fois le chiffre 1 à la même position sinon on y mettra 0. On commencera à lire les positions à partir de la droite. Exemples M[5 , 3] aura la valeur 1 car les deux représentations binaires ont le chiffre 1 à la première position. En effet : 5 = (101)2 et 3 (11)2 M[9 , 4] aura la valeur 0 car les deux représentations binaires n'ont pas de 1 à la même place. En effet : 9 = (1001)2 et 4 = (100)2 On se propose ensuite de chercher tous les chemins rectilignes menant de la première ligne à la dernière ligne en n'empruntant que des cellules contenant des 1 et en sautant au maximum une seule cellule contenant 0. Par conséquent, un chemin rectiligne est une colonne ne comportant pas deux cellules consécutives contenant 0. Pour tout chemin trouvé, on affichera son numéro (l'indice j). En plus, les données relatives à ce problème seront enregistrées dans un fichier texte intitulé chemins.txt et placé sur la racine du disque D. Ce fichier comportera dans sa première ligne le naturel p suivi d'une espace, suivie du naturel q et comportera dans chacune des lignes qui suivent le numéro du chemin trouvé. La dernière ligne contiendra le nombre de chemins trouvés.
Solution Algorithmique
Dans cet algorithme, On va utiliser quatre fonctions et sept procédures :
- la fonction saisie()
- la fonction convertir_binaire()
- la fonction test_position1()
- la fonction test_cellule()
- la procédure remplir_matrice()
- la procédure afficher_matrice()
- la procédure remplir_fichier_chemin()
Algorithme du programme Principal
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
Algorithme chemins_matrice Debut # Saisie des dimensions p et q p = saisie(5, 32) q = saisie(p, 32) # Remplir la matrice selon la règle définie remplir_matrice(m, p, q) # Afficher la matrice afficher_matrice(m, p, q) # Générer le fichier chemins.txt contenant les chemins remplir_fichier_chemin(m, p, q) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| p | entier |
| q | entier |
| m (matrice) | tableau T de 32 lignes x 32 colonnes d’entiers. |
La fonction saisir
La fonction saisie(inf, sup) sert à obliger l’utilisateur à entrer un nombre entier compris entre deux bornes :
inf : la borne inférieure (minimum autorisé)
sup : la borne supérieure (maximum autorisé)
Elle garantit que la valeur saisie est correcte.
La fonction demande d’abord à l’utilisateur d’entrer un entier dans l’intervalle [inf, sup].
Tant que l’utilisateur entre une valeur en dehors de l’intervalle, la fonction répète la saisie.
Dès qu’un nombre valide est fourni (inf ≤ n ≤ sup), la fonction le renvoie.
|
1 2 3 4 5 6 7 8 9 10 |
Fonction saisie(inf:entier, sup:entier): entier Ecrire('donner n tel que ' + inf + '<=n<=' + sup + ': ') lire (n) # Tant que la valeur n'est pas dans l’intervalle demandé, on redemande Tant que (n < inf) ou (n > sup) faire Ecrire('donner n tel que ' + inf + '<=n<=' + sup + ': ') lire (n) Fin tant que retourner n fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La fonction convertir_binaire
La fonction convertir_binaire(n) sert à transformer un nombre entier positif en une chaîne représentant son écriture en binaire.
1- On initialise une chaîne vide qui contiendra le résultat binaire.
2- Tant que n > 0 :
- On calcule le reste de la division par 2 → c’est le prochain bit (0 ou 1).
- On ajoute ce bit au début de la chaîne binaire.
- On divise n par 2 (division entière).
3- Quand n atteint 0, la chaîne contient le nombre en binaire → on la retourne.
|
1 2 3 4 5 6 7 8 9 10 |
Fonction convertir_binaire(n:entier):entier binaire <- '' # Construction de la chaîne en binaire Tant que n > 0 faire reste <- n mod 2 # Bit extrait (0 ou 1) binaire <- str(reste) + binaire # Ajout au début de la chaîne n = n div 2 # Division entière Fin tant que retourner binaire Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| binaire | chaîne |
| reste | chaîne |
La fonction test_position1
Cette fonction sert à vérifier si deux nombres binaires (sous forme de chaînes) possèdent un bit ‘1’ aligné sur la même position en partant de la droite.
On commence à comparer les deux chaînes au dernier caractère (bit de poids faible).
1- Tant que : (ch1[pos1] == '0' ou ch2[pos2] == '0') et que l’on n’est pas encore au début des chaînes
on recule d’un pas (pos1 −= 1, pos2 −= 1).
2- Quand la boucle s’arrête, on vérifie : le bit actuel de ch1 est ‘1’ et le bit actuel de ch2 est ‘1’
3- Si les deux sont ‘1’, la fonction renvoie Vrai, sinon Faux.
|
1 2 3 4 5 6 7 8 9 10 11 |
Fonction test_position1(ch1:chaine, ch2:chaine):booleen pos1 <- long(ch1) - 1 # Dernier indice de ch1 pos2 <- long(ch2) - 1 # Dernier indice de ch2 # On recule tant que les deux bits sont 0 Tant que (ch1[pos1] = '0' ou ch2[pos2] == '0') et pos1 > 0 et pos2 > 0 faire pos1 <- pos1 - 1 pos2 <- pos2 - 1 Fin tant que # Retourne vrai si les deux bits rencontrés sont '1' retourner ch1[pos1] = '1' et ch2[pos2] = '1' Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| pos1 | entier |
| pos2 | entier |
La fonction test_cellule
La fonction test_cellule sert à :
1. Convertir deux entiers i et j en binaire en utilisant la fonction convertir_binaire pour obtenir la représentation binaire de chacun des deux nombres.
2. Gérer le cas particulier du nombre 0 : si convertir_binaire renvoie une chaîne vide (ce qui arrive généralement lorsque le nombre vaut 0), la fonction remplace cette chaîne vide par "0" pour que le binaire soit correct.
3. Comparer les deux nombres binaires bit à bit
La fonction renvoie le résultat de test_position1(binaire_i, binaire_j).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
Fonction test_cellule (i:entier;j:entier): booleen binaire_i <- convertir_binaire(i) binaire_j <- convertir_binaire(j) # Si i ou j vaut 0 → chaîne vide, donc on remplace par "0" Si binaire_i = '' alors binaire_i <- '0' Fin si Si binaire_j = '' alors binaire_j = '0' Finsi retourner test_position1(binaire_i, binaire_j) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| binaire_i | chaîne |
| binaire_j | chaîne |
La procédure remplir_matrice
Cette procédure sert à remplir une matrice m de dimensions p × q en mettant dans chaque cellule 0 ou 1 suivant un test logique effectué par la fonction test_cellule(i, j).
1. Parcourir toute la matrice
Les deux boucles for permettent de parcourir toutes les lignes : i va de 0 à p-1 et toutes les colonnes : j va de 0 à q-1
2. Tester chaque couple (i, j)
Pour chaque cellule de coordonnées (i, j), la fonction appelle : test_cellule(i, j)
3. Remplir la matrice avec 0 ou 1 selon le résultat obtenu :
Si test_cellule(i, j) est vrai → la cellule prend la valeur 1
Sinon → la cellule prend la valeur 0
|
1 2 3 4 5 6 7 8 9 10 11 |
Procédure remplir_matrice(m:matrice; p:entier; q:entier) : Pour i de 0 à p-1 faire Pour j de 0 à q-1 faire Si test_cellule(i, j) alors m[i][j] <- 1 sinon m[i][j] <- 0 Finsi Finpour Finpour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| j | entier |
La procédure afficher_matrice
La procédure afficher_matrice sert à afficher le contenu de la matrice m de dimensions p × q sous forme de tableau bien structuré.
|
1 2 3 4 5 6 7 8 9 |
Procédure afficher_matrice(m, p, q) Ecrire('Matrice m') Pour i de 0 à p-1 faire Pour j de 0 à q-1 faire Ecrire(m[i][j]) Finpour Ecrire() Finpour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| j | entier |
La procédure remplir_fichier_chemin
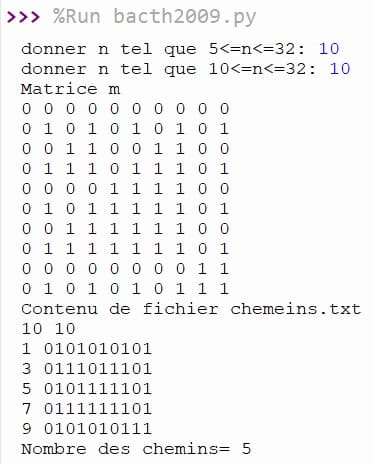
Cette procédure analyse la matrice m (de taille p × q) colonne par colonne pour rechercher des chemins, et écrit les résultats dans un fichier texte nommé chemins.txt.
1. La procédure ouvre le fichier chemins.txt en écriture et commence par y inscrire p q pour indiquer les dimensions de la matrice.
2. Analyse colonne par colonne
Pour chaque colonne j :
a- Elle vérifie si cette chaîne ne contient pas "00" en utilisant la fonction prédéfinie Pos(). Cela signifie qu’il n’y a aucun bloc de deux zéros consécutifs, donc la colonne est considérée comme un chemin valide.
b- Elle construit une chaîne ch constituée de tous les éléments de cette colonne, du haut vers le bas.
Si c’est un chemin valide : la colonne et sa chaîne binaire sont affichées, puis écrites dans le fichier texte.
3. Comptage des chemins
Un compteur (compteur_chemins) est incrémenté pour chaque colonne valide.
À la fin, le programme écrit dans le fichier le nombre des chemins
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 |
Procédure remplir_fichier_chemin(m:matrice; p:entier q:entier) Ouvrir("chemins.txt", f , "w") # Fichier texte pour les statistiques Ecrire('Contenu du fichier chemins.txt :') Ecrire(p + ' ' + q) # Écrire les bornes en première ligne Ecrire(f , p + ' ' + q + '\n') compteur_chemins <- 0 # Analyse colonne par colonne Pour j de 0 à q-1 faire ch <- '' # Construire la chaîne verticale de la colonne j Pour i de 0 à p-1 faire ch <- ch + Convch((m[i][j])) Finpour # Vérifier si la chaîne ne contient pas "00" Si Pos(ch,'00') < 0 alors Ecrire(j + ' ' + ch) Ecrire(f,j + ' ' + ch + '\n') compteur_chemins <- compteur_chemins+1 Finsi Fin pour # Écriture du nombre total de chemins Ecrire('Nombre des chemins = ' + Convch(compteur_chemins)) Ecrire(f,'Nombre des chemins = ' + Convch(compteur_chemins) + '\n') Fermer(f) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| f | fichier du chemins.txt |
| i | entier |
| j | entier |
| ch | chaîne |
| compteur_chemins | entier |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 |
from numpy import * lignes = 32 colonnes = 32 # Création d'une matrice 32x32 initialisée avec des entiers (par défaut = 0) # Cette matrice servira à stocker des valeurs 0 ou 1 m = array([[int()] * colonnes] * lignes) # --------------------------------------------------------- # Fonction pour saisir un nombre n dans l’intervalle [inf, sup] # --------------------------------------------------------- def saisie(inf, sup): # Première saisie de l'utilisateur n = int(input('donner n tel que ' + str(inf) + '<=n<=' + str(sup) + ': ')) # Tant que la valeur n'est pas dans l’intervalle demandé, on redemande while (n < inf) or (n > sup): n = int(input('donner n tel que ' + str(inf) + '<=n<=' + str(sup) + ': ')) return n # Retourner la valeur correcte # --------------------------------------------------------- # Fonction qui convertit un entier décimal en binaire (chaîne) # Exemple : 6 → "110" # --------------------------------------------------------- def convertir_binaire(n): binaire = '' # Construction de la chaîne en binaire while n > 0: reste = n % 2 # Bit extrait (0 ou 1) binaire = str(reste) + binaire # Ajout au début de la chaîne n = n // 2 # Division entière return binaire # --------------------------------------------------------- # Test si les deux chaînes binaires ont un '1' aligné # sur la même position en partant de la droite # --------------------------------------------------------- def test_position1(ch1, ch2): pos1 = len(ch1) - 1 # Dernier indice de ch1 pos2 = len(ch2) - 1 # Dernier indice de ch2 # On recule tant que les deux bits sont 0 while (ch1[pos1] == '0' or ch2[pos2] == '0') and pos1 > 0 and pos2 > 0: pos1 -= 1 pos2 -= 1 # Retourne vrai si les deux bits rencontrés sont '1' return ch1[pos1] == '1' and ch2[pos2] == '1' # --------------------------------------------------------- # Fonction qui teste si la cellule (i,j) doit contenir 0 ou 1 # selon les positions des '1' dans les binaire de i et j # --------------------------------------------------------- def test_cellule(i, j): binaire_i = convertir_binaire(i) binaire_j = convertir_binaire(j) # Si i ou j vaut 0 → chaîne vide, donc on remplace par "0" if binaire_i == '': binaire_i = '0' if binaire_j == '': binaire_j = '0' return test_position1(binaire_i, binaire_j) # --------------------------------------------------------- # Remplir la matrice m par des 0 ou 1 selon test_cellule # --------------------------------------------------------- def remplir_matrice(m, p, q): for i in range(p): for j in range(q): if test_cellule(i, j): m[i][j] = 1 else: m[i][j] = 0 # --------------------------------------------------------- # Affichage de la matrice sur l’écran # --------------------------------------------------------- def afficher_matrice(m, p, q): print('Matrice m') for i in range(p): for j in range(q): print(str(m[i][j]), end=' ') print() # --------------------------------------------------------- # Fonction qui écrit dans un fichier les "chemins" # Un chemin est une colonne dont la chaîne ne contient pas "00" # --------------------------------------------------------- def remplir_fichier_chemin(m, p, q): f = open("chemins.txt", "w") # Ouverture du fichier en écriture print('Contenu du fichier chemins.txt :') # Écrire les bornes en première ligne print(str(p) + ' ' + str(q)) f.write(str(p) + ' ' + str(q) + '\n') compteur_chemins = 0 # Analyse colonne par colonne for j in range(q): ch = '' # Construire la chaîne verticale de la colonne j for i in range(p): ch = ch + str(m[i][j]) # Vérifier si la chaîne ne contient pas "00" if ch.find('00') < 0: print(str(j) + ' ' + ch) f.write(str(j) + ' ' + ch + '\n') compteur_chemins += 1 # Écriture du nombre total de chemins print('Nombre des chemins = ' + str(compteur_chemins)) f.write('Nombre des chemins = ' + str(compteur_chemins) + '\n') f.close() # --------------------------------------------------------- # PROGRAMME PRINCIPAL # --------------------------------------------------------- # Saisie des dimensions p et q p = saisie(5, 32) q = saisie(p, 32) # Remplir la matrice selon la règle définie remplir_matrice(m, p, q) # Afficher la matrice afficher_matrice(m, p, q) # Générer le fichier contenant les chemins remplir_fichier_chemin(m, p, q) |
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés