Nombres circulaires – Bac pratique – Section informatique – 2012

Sujet (Algo et programmation - Bac 2012)
Un nombre premier N est dit circulaire s'il vérifie la propriété suivante : chacune des rotations de ses chiffres d'un élément vers la droite, forme à son tour un nombre premier.
Exemples :
- Si N = 719, N est un nombre premier circulaire car 719, 971 et 197 sont des nombres premiers, avec :
971 est le nombre obtenu après une rotation des chiffres de 719 d'un élément vers la droite,
et 197 est le nombre obtenu après une rotation des chiffres de 971 d'un élément vers la droite.
- Si N = 23, N n'est pas un nombre premier circulaire car il est premier mais 32 ne l'est pas.
- Si N = 6102, N n'est pas un nombre premier circulaire car il n'est pas premier.
Travail à faire :
Ecrire un programme Python et l'enregistrer sous le nom PremCirc, permettant :
de chercher tous les nombres premiers circulaires se trouvant dans un intervalle [p,ce (avec p et q sont deux entiers donnés tels que (10 < p < q < 20000) et les sauvegarder dans un fichier intitulé "Circul.dat".
d'afficher le contenu du fichier "Circul.dat".
Solution Algorithmique
Dans cet algorithme, On va utiliser trois fonctions et une procédure:
- la fonction saisie()
- la fonction test_premier()
- la fonction test_circulaire()
- la procédure remplir_fichier_circul()
Algorithme du programme Principal
|
1 2 3 4 5 6 7 8 9 |
Algorithme PremCirc Debut # Saisie de la borne inférieure p (10 < p < 20000) p = saisie(10, 20000) # Saisie de la borne supérieure q (p < q < 20000) q = saisie(p, 20000) # Remplissage du fichier avec les nombres premiers circulaires remplir_fichier_circul(p, q) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| p | entier |
| q | entier |
La fonction saisie
Cette fonction permet de saisir un entier n compris strictement entre deux bornes inf et sup.
Plus précisément :
Elle demande à l’utilisateur de saisir une valeur entière n.
Elle vérifie que n appartient à l’intervalle ]inf , sup[.
Tant que la valeur saisie est inférieure ou égale à inf ou supérieure ou égale à sup, la saisie est redemandée.
Lorsque la valeur est correcte, la fonction la retourne.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
Fonction saisie(inf:entier ; sup:entier):entier # Première saisie de l'entier Ecrire('donner n tel que ' , inf , '< n < ' , sup , ': ') Lire(n) # Tant que n n'est pas dans l'intervalle demandé, # on redemande la saisie Tant que (n <= inf) ou (n >= sup) faire Ecrire('donner n tel que ' , inf , '< n < ' , sup , ': ') Lire(n) Fin tant que # Retourne la valeur correcte saisie retourner n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | chaîne |
La fonction test_premier
La fonction test_premier(n) a pour rôle est de vérifier si un entier n est un nombre premier.
Plus précisément, la fonction :
- teste les diviseurs possibles de n à partir de 2 ;
- cherche un diviseur tant que n n’est pas divisible par i et que i ne dépasse pas la moitié de n ;
- conclut que n est premier si aucun diviseur n’a été trouvé ;
- retourne Vrai si n est premier et Faux dans le cas contraire.
|
1 2 3 4 5 6 7 8 9 10 |
Fonction test_premier(n:entier): booleen i <- 2 # Recherche d'un diviseur de n # tant que i ne divise pas n et que i <= n//2 Tant que (n div i != 0 et i <= n // 2) faire i <- i + 1 Fin tant que # Si aucun diviseur n'a été trouvé, n est premier retourner n mod i != 0 Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
La fonction test_circulaire
Ce programme définit la fonction facteur_premiers(n) dont le rôle est de décomposer un entier n en facteurs premiers et de retourner cette décomposition sous forme d’une chaîne de caractères.
Plus précisément, la fonction :
- teste successivement les diviseurs entiers à partir de 2 ;
- décompose n en facteurs premiers en divisant n chaque fois qu’un diviseur est trouvé ;
- compte le nombre de répétitions (puissance) de chaque facteur premier ;
- construit une chaîne représentant la décomposition sous la forme : nombre_d’occurrences suivi du facteur (exemple : 2² × 3 devient "223" ou 12 = 2² × 3¹ devient "2231") ;
- retourne la chaîne finale contenant toute la décomposition.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
Fonction test_circulaire(n:entier): booeen ch <- Conch(n) # Conversion du nombre en chaîne de caractères test <- Vrai # Variable booléenne pour indiquer si le nombre est circulaire i <- 0 # Compteur de rotations # Tant qu'il reste des rotations à tester et que le test est valide Tant que (i < long(ch)) et (test = Vrai) faire ch2 <- '' # Chaîne qui va contenir la rotation j <- 0 # Construction d'une rotation de la chaîne Tant que (j < long(ch)) faire ch2 <- ch2 + ch[j - i] j <- j + 1 Fin tant que # Vérification si la rotation obtenue est un nombre premier Si Non(test_premier(int(ch2))): test <- Faux Fin si i = i + 1 Fin tant que # Retourne Vrai si toutes les rotations sont premières retourner test = Vrai Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| ch | chaîne |
| test | booleen |
| ch2 | chaîne |
La procédure remplir_fichier_circul
La procédure remplir_fichier_circul(p, q) a pour rôle est de déterminer et enregistrer tous les nombres premiers circulaires compris entre deux entiers p et q.
Plus précisément, cette procédure :
- affiche un message indiquant le début du remplissage
- ouvre le fichier Circul.dat en mode écriture
- parcourt tous les entiers de p à q (bornes incluses)
- teste pour chaque entier s’il est premier circulaire à l’aide de la fonction test_circulaire()
- affiche chaque nombre premier circulaire trouvé
- écrit chaque nombre premier circulaire dans le fichier, un nombre par ligne
- ferme le fichier après la fin du traitement
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
Procédure remplir_fichier_circul(p:entier, q:entier) Ecrire('*** Remplir le fichier Circul.dat ***') # Ouverture du fichier en mode écriture Ouvrir(f , "Circul.dat", "w") # Parcours des entiers de p à q Pour i de p à q faire # Test si le nombre est premier circulaire Si test_circulaire(i) alors Ecrire(i) # Affichage du nombre Ecrire(f , Conch(i) + '\n') # Écriture dans le fichier Fin si Fin pour # Fermeture du fichier Fermer(f) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| f | fichier |
| i | entier |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 |
# -------------------------------------------------- # Fonction qui permet de saisir un entier n # compris strictement entre inf et sup # -------------------------------------------------- def saisie(inf, sup): # Demande à l'utilisateur de saisir un entier n n = int(input('donner n tel que ' + str(inf) + '< n < ' + str(sup) + ': ')) # Tant que n n'appartient pas à l'intervalle ]inf , sup[ # on redemande la saisie while (n <= inf) or (n >= sup): n = int(input('donner n tel que ' + str(inf) + '< n < ' + str(sup) + ': ')) # Retourne la valeur correcte saisie return n # -------------------------------------------------- # Fonction qui teste si un nombre n est premier # -------------------------------------------------- def test_premier(n): i = 2 # Recherche d'un diviseur de n # tant que i ne divise pas n et que i <= n//2 while (n % i != 0 and i <= n // 2): i = i + 1 # Si aucun diviseur n'a été trouvé, n est premier return n % i != 0 # -------------------------------------------------- # Fonction qui teste si un nombre est premier circulaire # (toutes ses rotations sont des nombres premiers) # -------------------------------------------------- def test_circulaire(n): ch = str(n) # Conversion du nombre en chaîne de caractères test = True # Variable booléenne pour indiquer si le nombre est circulaire i = 0 # Compteur de rotations # Tant qu'il reste des rotations à tester et que le test est valide while (i < len(ch)) and (test == True): ch2 = '' # Chaîne qui va contenir la rotation j = 0 # Construction d'une rotation de la chaîne while (j < len(ch)): ch2 = ch2 + ch[j - i] j = j + 1 # Vérification si la rotation obtenue est un nombre premier if not(test_premier(int(ch2))): test = False i = i + 1 # Retourne True si toutes les rotations sont premières return test == True # -------------------------------------------------- # Fonction qui remplit le fichier "Circul.dat" # par les nombres premiers circulaires compris # entre p et q # -------------------------------------------------- def remplir_fichier_circul(p, q): print('*** Remplir le fichier Circul.dat ***') # Ouverture du fichier en mode écriture f = open("Circul.dat", "w") # Parcours des entiers de p à q for i in range(p, q + 1): # Test si le nombre est premier circulaire if test_circulaire(i): print(i) # Affichage du nombre f.write(str(i) + '\n') # Écriture dans le fichier # Fermeture du fichier f.close() # -------------------------------------------------- # Programme principal # -------------------------------------------------- # Saisie de la borne inférieure p (10 < p < 20000) p = saisie(10, 20000) # Saisie de la borne supérieure q (p < q < 20000) q = saisie(p, 20000) # Remplissage du fichier avec les nombres premiers circulaires remplir_fichier_circul(p, q) |
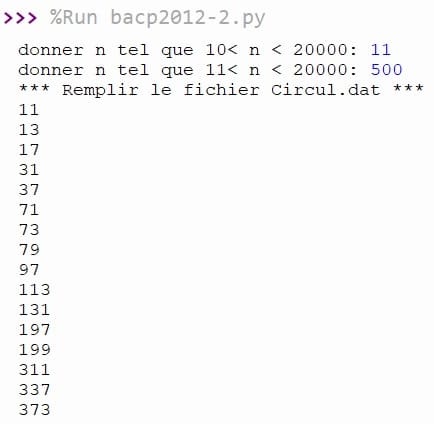
Exécution du programme
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés


















