Calcul d’aires – Bac théorique – Section informatique – 2025

Sujet (Algo et programmation - Bac 2025)
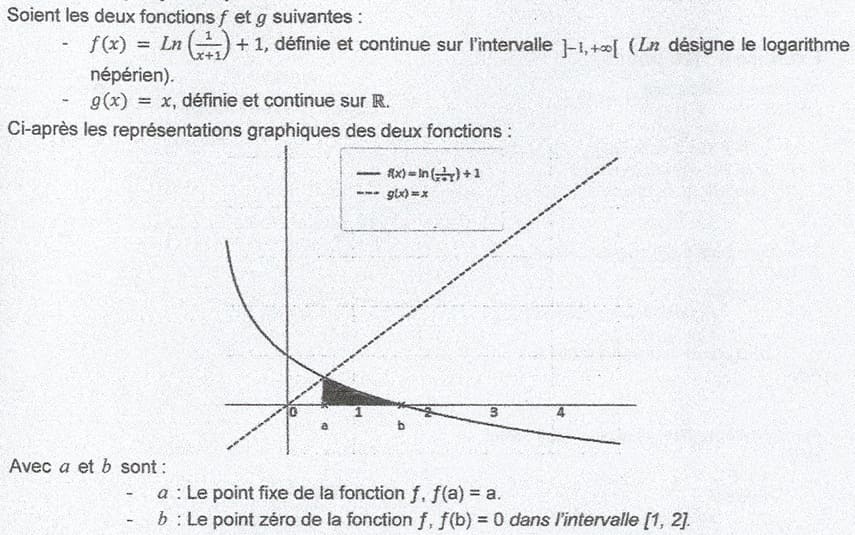
Avec a et b sont :
- a Le point fixe de la fonction f, f(a)= a.
- b Le point zéro de la fonction f, f (b) = 0 dans l'intervalle [1, 21
Soit ![]() l'aire de la partie grisée. Afin d'étudier la convergence des approximations de cette aire par les méthodes "rectangles à gauche" et "rectangles à droite" vers celle des "rectangles du point milieu", on se propose d'écrire un programme permettant de réaliser les tâches suivantes :
l'aire de la partie grisée. Afin d'étudier la convergence des approximations de cette aire par les méthodes "rectangles à gauche" et "rectangles à droite" vers celle des "rectangles du point milieu", on se propose d'écrire un programme permettant de réaliser les tâches suivantes :
- La saisie d'un réel epsilon positif et inférieur ou égal à 10-4.
- La recherche du point fixe de f (le point a) à epsilon près.
- La recherche du point zéro de f (le point b) à epsilon près.
- La génération d'un fichier d'enregistrements "Calcul.dat" sur la racine du disque C où
chaque enregistrement est formé par les champs suivants :
- n : le nombre des subdivisions dans l'intervalle [a, b].
- rd : l'aire A calculée par la méthode des rectangles à droite avec n
- rg l'aire A calculée par la méthode des rectangles à gauche avec n
- rm : l'aire A calculée par la méthode des rectangles du point milieu avec n subdivisions.
NB :
Le traitement s'arrête lorsque la moyenne des aires calculées par les deux méthodes rectangles à droite et rectangles à gauche converge vers l'aire calculée par la méthode des rectangles du point milieu à epsilon près, c'est à dire :
![]()
n est initialisé à I et s'incrémente jusqu'à la condition d'arrêt.
Le candidat peut utiliser la fonction Ln(x), sans la développer, pour calculer le logarithme népérien de x.
Travail demandé
1) Ecrire un algorithme du programme principal en le décomposant en modules permettant de réaliser les tâches décrites précédemment.
2) Ecrire un algorithme pour chaque module envisagé.
Solution Algorithmique
Dans cet algorithme, On va utiliser huit fonctions et deux procédures :
- la fonction saisie()
- la fonction f()
- la fonction pgcd()
- la fonction point_fixe()
- la fonction point_zero()
- la fonction rectangleD()
- la fonction rectangleG()
- la fonction rectangleM()
- la procédure generer()
- la procédure afficher_fichier()
Algorithme du programme Principal
|
1 2 3 4 5 6 7 8 |
Algorithme calcu_aires Debut epsilon <- saisie() # Saisie de la précision a <- point_fixe(epsilon) # Calcul du point fixe b <- point_zero(epsilon) # Calcul du point zéro generer(a, b, epsilon) # Calcul et sauvegarde des intégrales afficher_fichier() # Affichage des résultats Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| epsilon | réel |
| a | réel |
| b | réel |
La fonction saisie
Cette fonction permet de saisir et retourner un réel <= 10-4 en contrôlant la validité de la saisie.
|
1 2 3 4 5 6 7 8 9 10 |
Fonction saisie():reel Ecrire('donner epsilon telque 0 < epsilon <= 0.0001: ') Lire(epsilon) # Tant que la valeur saisie n’est pas valide, on redemande Tant que Non(0 < epsilon <= 0.0001) faire Ecrire('donner epsilon telque 0 < epsilon <= 0.0001: ') Lire(epsilon) Fin tant que retourner epsilon Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| epsilon | entier |
La fonction f
cette fonction prend un nombre x et renvoie une valeur obtenue par une transformation logarithmique.
|
1 2 3 |
Fonction f(x:reel):reel retourner Ln(1/(1+x)) + 1 Fin |
La fonction point_fixe
Cette fonction permet de déterminer, par la méthode du point fixe, une solution approchée de l’équation 𝑥=𝑓(𝑥) à une précision epsilon donnée.
|
1 2 3 4 5 6 7 8 9 10 |
Fonction point_fixe(epsilon:reel):reel xa <- 0 # Valeur actuelle xp <- xa # Valeur précédente # Répéter tant que la précision epsilon n’est pas atteinte Tant que abs(xa - xp) > epsilon faire xp <- xa xa <- f(xp) Fin tant que retourner xa Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| xa | réel |
| xp | réel |
La fonction point_zero
Cette fonction a pour rôle de calculer une valeur approchée du point zéro (racine) de la fonction 𝑓(𝑥) en utilisant la méthode de dichotomie.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
Fonction point_zero(epsilon:reel):reel a <- 1 b <- 2 m <- (a + b) / 2 # Continuer tant que f(m) ≠ 0 et que l’intervalle est assez grand Tant que (f(m) != 0) et (b - a >= epsilon) faire m = (a + b) / 2 # Choix du sous-intervalle contenant la racine Si f(a) * f(m) > 0 alors a <- m Sinon b <- m Fin si Fin tant que retourner m Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| a | réel |
| b | réel |
| m | réel |
La fonction rectangleD
Cette fonction permet de calculer une valeur approchée de l’intégrale de 𝑓(𝑥) sur [𝑎,𝑏] par la méthode des rectangles à droite, en utilisant n rectangles.
|
1 2 3 4 5 6 7 8 9 10 |
Fonction rectangleD(a:reel, b:reel, n:entier):reel s <- 0 h <- (b - a) / n # Largeur d’un rectangle x <- a + h Pour i de 1 à n faire s <- s + f(x) x <- x + h Fin pour retourner s * h Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| h | réel |
| x | réel |
La fonction rectangleG
Cette fonction permet de calculer une valeur approchée de l’intégrale de 𝑓(𝑥) sur [𝑎,𝑏] par la méthode des rectangles à gauche, en utilisant n rectangles.
|
1 2 3 4 5 6 7 8 9 10 |
Fonction rectangleG(a:reel, b:reel, n:entier):reel s <- 0 h <- (b - a) / n # Largeur d’un rectangle x <- a Pour i de 1 à n faire s <- s + f(x) x <- x + h Fin pour retourner s * h Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| h | réel |
| x | réel |
La fonction rectangleM
Cette fonction a pour rôle de calculer une valeur approchée de l’intégrale de la fonction 𝑓(𝑥) sur l’intervalle [𝑎,𝑏] en utilisant la méthode des rectangles au milieu.
|
1 2 3 4 5 6 7 8 9 10 |
Fonction rectangleM(a:reel, b:reel, n:entier):reel s <- 0 h <- (b - a) / n # Largeur d’un rectangle x <- a + h / 2 Pour i de 1 à n faire s <- s + f(x) x <- x + h Fin pour retourner s * h Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| h | réel |
| x | réel |
La procédure generer
Cette procédure a pour rôle de calculer des approximations successives de l’intégrale de la fonction f(x) sur l’intervalle [𝑎,𝑏], d’augmenter progressivement la précision, puis de sauvegarder les résultats dans un fichier binaire.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
Procédure generer(a:reel, b:reel, epsilon:reel) Ouvrit(fc , "wb") # Ouverture du fichier en écriture binaire e.n <- 1 e.rd <- rectangleD(a, b, e.n) e.rg <- rectangleG(a, b, e.n) e.rm <- rectangleM(a, b, e.n) # Augmenter n tant que la précision demandée n’est pas atteinte Tant que abs(((e.rd + e.rg) / 2) - e.rm) > epsilon faire e.n <- e.n + 1 e.rd <- rectangleD(a, b, e['n']) e.rg <- rectangleG(a, b, e['n']) e.rm <- rectangleM(a, b, e['n']) # Sauvegarde des résultats dans le fichier Ecrire(e, fc) Fin tant que Fermer(fc) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| e | enregistrement |
| fc | fichier |
La procédure afficher_fichier
Cette procédure a pour rôle de lire le contenu du fichier binaire calcul.dat et d’afficher à l’écran les résultats stockés.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
Procedure afficher_fichier() Ecrire('Contenu du fichier calcul.dat') Ouvrir(fc , "rb") Tant que Vrai faire Essayer: # Lecture d’un enregistrement Lire(e,fc) Ecrire(e.n, ' ', e.rd, ' ', e.rg, ' ', e.rm) En cas de fin fichier: # Fin du fichier sortir Fin tant que Fermer(fc) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| e | enregistrement |
| fc | fichier |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 |
import math from pickle import load, dump # Import des fonctions : # - dump : pour enregistrer des données dans un fichier # - load : pour lire des données depuis un fichier # -------------------------------------------------- # Enregistrement pour stocker les résultats des calculs # n : nombre de subdivisions # rd : valeur de l’intégrale par la méthode des rectangles à droite # rg : valeur de l’intégrale par la méthode des rectangles à gauche # rm : valeur de l’intégrale par la méthode des rectangles au milieu # -------------------------------------------------- e = dict( n=int(), rd=float(), rg=float(), rm=float ) # -------------------------------------------------- # Fonction de saisie de epsilon # epsilon doit vérifier : 0 < epsilon <= 0.0001 # -------------------------------------------------- def saisie(): epsilon = float(input('donner epsilon telque 0 < epsilon <= 0.0001: ')) # Tant que la valeur saisie n’est pas valide, on redemande while not (0 < epsilon <= 0.0001): epsilon = float(input('donner epsilon telque 0 < epsilon <= 0.0001: ')) return epsilon # -------------------------------------------------- # Fonction mathématique f(x) # -------------------------------------------------- def f(x): return math.log(1/(1+x)) + 1 # -------------------------------------------------- # Calcul du point fixe par la méthode des itérations # -------------------------------------------------- def point_fixe(epsilon): xa = 0 # Valeur actuelle xp = xa # Valeur précédente # Répéter tant que la précision epsilon n’est pas atteinte while abs(xa - xp) > epsilon: xp = xa xa = f(xp) return xa # -------------------------------------------------- # Calcul du point zéro par la méthode de dichotomie # -------------------------------------------------- def point_zero(epsilon): a = 1 b = 2 m = (a + b) / 2 # Continuer tant que f(m) ≠ 0 et que l’intervalle est assez grand while (f(m) != 0) and (b - a >= epsilon): m = (a + b) / 2 # Choix du sous-intervalle contenant la racine if f(a) * f(m) > 0: a = m else: b = m return m # -------------------------------------------------- # Méthode des rectangles à droite # -------------------------------------------------- def rectangleD(a, b, n): s = 0 h = (b - a) / n # Largeur d’un rectangle x = a + h for i in range(1, n + 1): s = s + f(x) x = x + h return s * h # -------------------------------------------------- # Méthode des rectangles à gauche # -------------------------------------------------- def rectangleG(a, b, n): s = 0 h = (b - a) / n x = a for i in range(1, n + 1): s = s + f(x) x = x + h return s * h # -------------------------------------------------- # Méthode des rectangles au milieu # -------------------------------------------------- def rectangleM(a, b, n): s = 0 h = (b - a) / n x = a + h / 2 for i in range(1, n + 1): s = s + f(x) x = x + h return s * h # -------------------------------------------------- # Génération et sauvegarde des résultats dans un fichier # -------------------------------------------------- def generer(a, b, epsilon): fc = open("calcul.dat", "wb") # Ouverture du fichier en écriture binaire e['n'] = 1 e['rd'] = rectangleD(a, b, e['n']) e['rg'] = rectangleG(a, b, e['n']) e['rm'] = rectangleM(a, b, e['n']) # Augmenter n tant que la précision demandée n’est pas atteinte while abs(((e['rd'] + e['rg']) / 2) - e['rm']) > epsilon: e['n'] = e['n'] + 1 e['rd'] = rectangleD(a, b, e['n']) e['rg'] = rectangleG(a, b, e['n']) e['rm'] = rectangleM(a, b, e['n']) # Sauvegarde des résultats dans le fichier dump(e, fc) fc.close() # -------------------------------------------------- # Lecture et affichage du contenu du fichier # -------------------------------------------------- def afficher_fichier(): print('Contenu du fichier calcul.dat') fc = open("calcul.dat", "rb") while True: try: # Lecture d’un enregistrement e = load(fc) print(e['n'], ' ', e['rd'], ' ', e['rg'], ' ', e['rm']) except EOFError: # Fin du fichier break fc.close() # -------------------------------------------------- # Programme principal # -------------------------------------------------- epsilon = saisie() # Saisie de la précision a = point_fixe(epsilon) # Calcul du point fixe b = point_zero(epsilon) # Calcul du point zéro generer(a, b, epsilon) # Calcul et sauvegarde des intégrales afficher_fichier() # Affichage des résultats |
Exécution du programme

0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés




















