Codage de Fibonacci – Bac théorique – Section informatique – 2016
Sujet (Algo et programmation - Bac 2016)
Le codage de Fibonacci est un code binaire, utilisant des termes de la suite de Fibonacci et servant essentiellement dans la compression de données.
Pour déterminer le code de Fibonacci d'un entier K strictement positif, on suit les étapes suivantes
Etape 1 : Déterminer la liste des termes de la suite de Fibonacci inférieurs ou égaux à K,
sachant que la suite de Fibonacci U est définie comme suit :
U,= 1, U2 = 1
Un = Uni + Un-2 pour n > 2
Etape 2 : Décomposer l'entier K en une somme des termes de la suite de Fibonacci déjà calculés dans l'étape précédente, tout en commençant par utiliser le plus grand terme inférieur à K et sans prendre en considération le premier ternie de la suite (U1).
Etape 3 : Former un code binaire à partir de la liste des termes calculée dans l'étape 1 et sans prendre en considération le premier terme de la suite (U1) : en concaténant le caractère "1" dans le cas où le terme a été utilisé dans la somme calculée au niveau de l'étape 2 et en concaténant le caractère "0" dans le cas contraire.
Etape 4 : Ajouter à la fin du code obtenu précédemment le caractère "1" pour obtenir le code de Fibonacci.
On se propose d'écrire un programme qui permet de saisir un entier K strictement positif et d'afficher le code de Fibonacci correspondant.
Exemple : Pour K = 50,
Etape 1 : La liste des termes de la suite de Fibonacci inférieurs ou égaux à 50 et sans prendre en considération le premier terme de la suite (U1) est : 1, 2, 3, 5, 8, 13, 21 et 34.
Etape 2 : La décomposition de K sera comme suit : 50 = 34 + 13 + 3
Etape 3 : Etant donnée la liste des termes obtenue dans l'étape 1 et sans prendre en considération le premier terme de la suite (U1) : 1, 2, 3, 5, 8, 13, 21 et 34
En concaténant le caractère "0" pour les termes 1, 2, 5, 8 et 21 qui n'ont pas été utilisés dans la somme et en concaténant le caractère "1" pour les termes 3, 13 et 34 qui ont été utilisés dans la somme, le code binaire formé est : 00100101
Etape 4 : En ajoutant à la fin du code binaire obtenu précédemment le caractère "1", le code de Fibonacci est : 001001011
Travail à faire :
- Analyser le problème en le décomposant en modules.
- Analyser chacun des modules envisagés.
Solution Algorithmique
Dans cet algorithme, On va utiliser trois fonctions et une procédure:
- la fonction saisie()
- la fonction termes_fibonacci()
- la procédure decomposition()
- la fonction code_fibonacci()
Algorithme du programme Principal
|
1 2 3 4 5 6 7 8 |
Algorithme Fac_Prim Debut longueur_tab <- 0 # initialisation du compteur de termes k <- saisie() # saisie de l'entier positif termes_fibonacci(t1, k) # remplir le tableau t1 avec les termes de Fibonacci decomposition(t1, t2, k, longueur_tab) # remplir t2 avec la décomposition binaire Ecrire(code_fibonacci(t2, longueur_tab)) # afficher le code de Fibonacci final Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| k | entier |
| longueur_tab | entier |
| t1 | tableau pour stocker les termes de Fibonacci (entiers) |
| t2 | tableau pour stocker le code binaire correspondant (chaînes) |
La fonction saisie
Cette fonction permet de saisir un entier strictement positif et assure que la valeur entrée respecte la condition k > 0.
1- Saisie initiale : la fonction demande à l’utilisateur de saisir un entier k avec la consigne k > 0.
2- Vérification de la validité : tant que l’utilisateur saisit un nombre inférieur ou égal à 0, la fonction redemande la saisie.
3- Retour de la valeur : une fois qu’un entier strictement positif est saisi, la fonction retourne cette valeur.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
Fonction saisie():entier # Saisie de l'entier par l'utilisateur Ecrire(('donner k tel que k>0 : ')) Lire(k) # Tant que k n'est pas strictement positif, redemander la saisie Tant que (k <= 0) faire Ecrire(('donner k tel que k>0 : ')) Lire(k) Fin pour # Retourner la valeur valide retourner k Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| k | entier |
La procédure termes_fibonacci
Cette procédure génère tous les termes de la suite de Fibonacci inférieurs à n et les stocke dans un tableau.
1- Initialisation :
Les deux premiers termes u1 et u2 sont fixés à 1.
Le troisième terme u3 est calculé comme u1 + u2.
Le premier terme (1) est stocké dans le tableau t[0].
longueur_tab est initialisée à 1 pour compter le nombre de termes stockés.
2- Génération des termes suivants :
Tant que le terme suivant u3 est inférieur à n, la suite est générée :
a) On déplace les valeurs : u1 ← u2, u2 ← u3, u3 ← u1 + u2.
b) Le compteur longueur_tab est incrémenté.
c) Le nouveau terme u3 est stocké dans le tableau t.
3- Résultat :
À la fin, le tableau t contient tous les termes de Fibonacci inférieurs à n.
La variable globale longueur_tab indique le nombre de termes stockés.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
Procedure termes_fibonacci(t:tableau,n:entier) u1 <- 1 # premier terme u2 <- 1 # deuxième terme u3 <- u1 + u2 # calcul du troisième terme t[0] <- 1 # stocker le premier terme longueur_tab <- 1 # initialisation du compteur de termes # Générer les termes de Fibonacci jusqu'à ce qu'ils soient inférieurs à n Tant que (u3 < n) faire u1 <- u2 u2 <- u3 u3 <- u2 + u1 longueur_tab <- longueur_tab + 1 t[longueur_tab] <- u3 # ajouter le terme au tableau Fin tant que Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| u1 | entier |
| u2 | entier |
| u3 | entier |
| longueur_tab | entier (variable globale) |
La procédure decomposition
Cette procédure permet de décomposer un entier n en somme de termes de Fibonacci et de créer le code binaire correspondant, où chaque bit indique si un terme est utilisé ('1') ou non ('0').
1- Initialisation du code binaire :
Tous les éléments du tableau t2 sont initialisés à '0'.
Chaque position de t2 correspond à un terme du tableau t1 contenant les termes de Fibonacci.
2- Utilisation du plus grand terme :
On commence par utiliser le plus grand terme de Fibonacci inférieur ou égal à n :
La différence à décomposer est calculée comme difference = n - t1[longueur_tab - 1].
Le bit correspondant à ce plus grand terme est mis à '1' dans t2.
3- Décomposition du reste :
Tant que la différence n’est pas nulle et qu’il reste des termes plus petits à considérer :
Si le terme courant t1[i] est inférieur ou égal à la différence, il est utilisé :
La différence est réduite : difference -= t1[i].
Le bit correspondant est mis à '1'. Sinon, le bit reste '0'.
On passe ensuite au terme de Fibonacci suivant, plus petit (i -= 1).
4- Résultat :
Le tableau t2 contient une représentation binaire de la décomposition de n en termes de Fibonacci : '1' si le terme est utilisé, '0' sinon.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
Procedure decomposition(t1:tableau, t2:tableau, n:entier, longueur_tab:entier): # Initialiser tout le code binaire à '0' Pour i de 0 à longueur_tab - 1 faire t2[i] <- '0' Fin pour # Calculer la différence à décomposer difference <- n - t1[longueur_tab - 1] # on utilise le plus grand terme # Marquer le plus grand terme utilisé dans la décomposition i <- longueur_tab - 2 t2[longueur_tab - 1] <- '1' # Décomposer le reste en utilisant les termes plus petits Tant que (difference != 0) et (i >= 0) faire Si difference >= t1[i] alors difference <- difference - t1[i] # soustraire le terme utilisé t2[i] <- '1' # marquer le terme comme utilisé Fin si i = i - 1 # passer au terme suivant plus petit Fin tant que Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| difference | entier |
| i | entier |
La fonction code_fibonacci
Cette fonction permet de construire et retourner le code binaire final de Fibonacci à partir d’un tableau de bits.
Plus précisément, elle reçoit t : un tableau contenant des caractères '0' et '1' représentant la décomposition de Fibonacci et n : le nombre de bits significatifs à utiliser dans ce tableau.
Elle concatène successivement les n premiers éléments du tableau t pour former une chaîne binaire.
Elle ajoute obligatoirement un '1' final, conformément à la règle du codage de Fibonacci (ce bit marque la fin du code).
Elle affiche un message indiquant que le code binaire de Fibonacci est en cours de génération.
Elle retourne la chaîne binaire finale correspondant au code de Fibonacci.
|
1 2 3 4 5 6 7 8 9 10 |
Fonction code_fibonacci(t:tableau, n:entier):chaine Ecrire('le code binaire de Fibonacci est : ', end='') code <- '' # Concaténer les '0' et '1' du tableau t Pour i de 0 à n-1 faire code <- code + t[i] code <- code + '1' # ajouter le '1' final obligatoire Fin pour retourner code Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| code | chaîne |
| i | entier |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 |
from numpy import * # -------------------------------------------------- # Déclaration des tableaux : # t1 : tableau pour stocker les termes de Fibonacci (entiers) # t2 : tableau pour stocker le code binaire correspondant (chaînes) # -------------------------------------------------- t1 = array([int()] * 100) t2 = array([str()] * 100) # -------------------------------------------------- # Fonction qui permet de saisir un entier k > 0 # -------------------------------------------------- def saisie(): # Saisie de l'entier par l'utilisateur k = int(input('donner k tel que k>0 : ')) # Tant que k n'est pas strictement positif, redemander la saisie while (k <= 0): k = int(input('donner k tel que k>0 : ')) # Retourner la valeur valide return k # -------------------------------------------------- # Procédure qui remplit le tableau t avec les termes # de la suite de Fibonacci inférieurs à n # -------------------------------------------------- def termes_fibonacci(t, n): global longueur_tab # variable globale pour stocker le nombre de termes u1 = 1 # premier terme u2 = 1 # deuxième terme u3 = u1 + u2 # calcul du troisième terme t[0] = 1 # stocker le premier terme longueur_tab = 1 # initialisation du compteur de termes # Générer les termes de Fibonacci jusqu'à ce qu'ils soient inférieurs à n while (u3 < n): u1 = u2 u2 = u3 u3 = u2 + u1 longueur_tab = longueur_tab + 1 t[longueur_tab] = u3 # ajouter le terme au tableau # -------------------------------------------------- # Procedure qui décompose l'entier n en somme de termes # de Fibonacci et remplit le tableau t2 avec '0' et '1' # -------------------------------------------------- def decomposition(t1, t2, n, longueur_tab): # Initialiser tout le code binaire à '0' for i in range(longueur_tab): t2[i] = '0' # Calculer la différence à décomposer difference = n - t1[longueur_tab - 1] # on utilise le plus grand terme # Marquer le plus grand terme utilisé dans la décomposition i = longueur_tab - 2 t2[longueur_tab - 1] = '1' # Décomposer le reste en utilisant les termes plus petits while (difference != 0) and (i >= 0): if difference >= t1[i]: difference = difference - t1[i] # soustraire le terme utilisé t2[i] = '1' # marquer le terme comme utilisé i = i - 1 # passer au terme suivant plus petit # -------------------------------------------------- # Fonction qui crée le code binaire final de Fibonacci # -------------------------------------------------- def code_fibonacci(t, n): print('le code binaire de Fibonacci est : ', end='') code = '' # Concaténer les '0' et '1' du tableau t for i in range(n): code = code + t[i] code = code + '1' # ajouter le '1' final obligatoire return code # -------------------------------------------------- # Programme principal # -------------------------------------------------- longueur_tab = 0 # initialisation du compteur de termes k = saisie() # saisie de l'entier positif termes_fibonacci(t1, k) # remplir le tableau t1 avec les termes de Fibonacci decomposition(t1, t2, k, longueur_tab) # remplir t2 avec la décomposition binaire print(code_fibonacci(t2, longueur_tab)) # afficher le code de Fibonacci final |
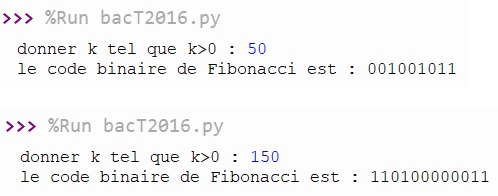
Exécution du programme
0 commentaire
laisser un commentaire
Passion de robotique
Tutoriels récents
Atelier robotique
Tutoriels populaires
Construction des robots
Tutoriels plus commentés
Bras robotique
Categories
Maison intelligente
