Conversion bases – Bac pratique – Section informatique – 2010
Sujet (Algo et programmation - Bac 2010)
Soit un fichier enregistré sous le nom nb_base.dat dans lequel on va enregistrer n chaînes de caractères. Chaque chaîne est formée de 5 caractères au maximum. Chacun de ces caractères est soit un chiffre, soit une lettre majuscule de l'intervalle "A".."F".Pour chaque chaîne du fichier nb_base.dat, on se propose de réaliser les tâches suivants :
- Déterminer la plus petit base b à laquelle, peut appartenir le nombre m représenté par la chaîne des caractères.
- Déterminer l'équivalent décimal d du nombre m
- Ranger dans une ligne d'un fichier texte nommé nombre.txt, la valeur décimale correspondante, de la façon suivante : (m)b=(d)10
Exemple :
Si le contenu du fichier nb_base.dat est le suivant :
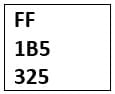
Le contenu du fichier nombre.txt est le sera :
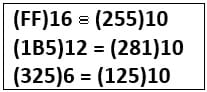
Remarque:
La plus petite base à laquelle appartient la valeur 1B5 est la base 12. En effet, le plus grand chiffre de ce nombre est B qui correspond à la valeur décimale 11.
De ce fait, la plus petite base est 1B5 est 11+1=12
Travail demandé:
Ecrire un programme en Python qui permet de :
- Saisir un entier 2<=n<=10. - Enregistrer dans un fichier nommé nb_base.dat n chaînes de caractères répondant aux conditions précédemment citées. - Remplir et afficher le fichier nombre.txt.
Solution Algorithmique
Dans cet algorithme, On va utiliser six fonctions et deux procédures :
- la fonction saisie_nbr_chaines()
- la fonction verif_chaine()
- la fonction saisie_chaine()
- la fonction recherche_base()
- la fonction exposant()
- la fonction conversion_decimale()
- la procédure remplir_fichiers()
- la procédure afficher_fichier()
Algorithme du programme Principal
|
1 2 3 4 5 6 7 |
Algorithme conversion_bases Debut n <- saisie_nbr_chaines() # Saisie du nombre de chaînes à traiter remplir_fichiers(n) # Génération des fichiers afficher_fichier("nb_base.dat") # Affichage du fichier nb_base.dat afficher_fichier("nombre.txt") # Affichage du fichier nombre.text Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La fonction saisie_nbr_chaines
Cette fonction demande à l’utilisateur de saisir un entier compris entre 2 et 10.
Tant que la valeur saisie n’est pas dans cet intervalle, la fonction redemande un nombre.
Elle garantit donc que le nombre retourné sera toujours un entier valide entre 2 et 10.
|
1 2 3 4 5 6 7 8 9 10 |
Fonction saisie_nbr_chaines(): entier Ecrire('donner n tel que 2<=n<=10: ') lire (n) # Tant que la valeur n'est pas dans l’intervalle demandé, on redemande Tant que (n < 2) ou (n > 10) faire Ecrire('donner n tel que 2<=n<=10: ') lire (n) Fin tant que retourner n fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La fonction verif_chaine
Cette fonction vérifie si une chaîne de caractères est valide selon deux conditions :
1. La chaîne doit avoir une longueur comprise entre 1 et 5 caractères.
2. Tous les caractères de la chaîne doivent appartenir à l’ensemble : des chiffres 0 à 9 et les lettres majuscules A à F
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
Fonction verif_chaine(ch:chaine):booleen Si 1 <= len(ch) <= 5 alors # Vérification de la longueur i <- 0 # Vérifier tous les caractères sauf le dernier Tant que (i < long(ch) - 1) et (('A' <= ch[i] <= 'F') ou ('0' <= ch[i] <= '9')) faire i <- i + 1 Fin tant que # Vérifier le dernier caractère retourner ('A' <= ch[i] <= 'F') ou ('0' <= ch[i] <= '9') Sinon retourner Faux Finsi Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
La fonction saisie_chaine
Cette fonction vérifie si une chaîne de caractères est valide selon deux conditions :
1. La chaîne doit avoir une longueur comprise entre 1 et 5 caractères.
2. Tous les caractères de la chaîne doivent appartenir à l’ensemble :
|
1 2 3 4 5 6 7 8 9 10 |
Fonction saisie_chaine(): chaine Ecrire(("donner une chaine au 5 caractéres max et formée des chiffres ou A..F: ")) lire(ch) # Tant que la chaîne est invalide on redemande Tant que verif_chaine(ch) = Faux faire Ecrire(("donner une chaine au 5 caractéres max et formée des chiffres ou A..F: ")) lire(ch) Fin tantque retourner ch Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| ch | chaîne |
La fonction recherche_base
Cette procédure sert à afficher la matrice M, qui contient les distances entre tous les points.
1- Elle affiche les noms des points (A, B, C, …) sur la première ligne.
2- Pour chaque point (ligne) : elle affiche d’abord son nom (A, B, C, …), puis toutes les distances entre ce point et les autres (m[i][j]).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
Fonction recherche_base(ch:chaine):entier max_chiffre <- ch[0] # Recherche du plus grand caractère Pour i de 1 à long(ch)-1 faire Si max_chiffre < ch[i] alors max_chiffre <- ch[i] Finsi Fin pour # Si le caractère est une lettre A..F Si 'A' <= max_chiffre <= 'F' alors retourner ord(max_chiffre) - 54 # Convertir A→10, B→11 ... F→15 Sinon retourner Valeur(max_chiffre) + 1 # Sinon base = chiffre + 1 Finsi Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| max_chiffre | entier |
La fonction exposant
Cette procédure sert à afficher la matrice M, qui contient les distances entre tous les points.
1- Elle affiche les noms des points (A, B, C, …) sur la première ligne.
2- Pour chaque point (ligne) : elle affiche d’abord son nom (A, B, C, …), puis toutes les distances entre ce point et les autres (m[i][j]).
|
1 2 3 4 5 6 7 |
Fonction exposant(n:entier;e:entier):entier p <- 1 Pour i de 0 à e-1 faire p <- p * n finpour retourner p Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| p | entier |
La fonction conversion_decimale
Ce programme sert à saisir un point valide, c’est-à-dire une lettre représentant un point parmi : A, B, C, …
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
Fonction conversion_decimale(ch:chaine, base:entier):entier nombre <- 0 Pour i de 0 à long(ch)-1 faire # Conversion du caractère en valeur numérique Si 'A' <= ch[i] <= 'F' alors x <- ord(ch[i]) - 55 # A=10, B=11, ..., F=15 Sinon x <- int(ch[i]) finsi # Ajout contribution du chiffre : valeur * base^(position) nombre = nombre + x * exposant(base, len(ch) - i - 1) finpour retourner nombre fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| nombre | entier |
| i | entier |
La fonction point_plus_proche
Cette fonction recherche et retourne le nom du point le plus proche d’un point donné, en comparant les distances contenues dans la matrice M.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
Fonction point_plus_proche(point:caractere, m:matrice, n:entier): caractere indice_proche <- 0 # Avancer jusqu'à trouver une distance différente de 0 (éviter A → A = 0) Tant que m[indice_proche][ord(point) - 65] == 0 faire indice_proche <- indice_proche + 1 Fin tant que # Recherche de la distance strictement minimale Pour i de 1 à n-1 faire Si (m[i][ord(point) - 65] != 0) et (m[i][ord(point) - 65] < m[indice_proche][ord(point) - 65]) alors indice_proche <- i Finsi Finpour # Retourne le nom du point correspondant retourner chr(indice_proche + 65) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| indice_proche | entier |
| i | entier |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 |
from numpy import * import random lignes = 50 colonnes = 50 # Matrice T : contient les coordonnées des points (t[0] = abscisses, t[1] = ordonnées) t = array([[int()] * colonnes] * lignes) # Matrice M : contiendra les distances entre tous les points m = array([[float()] * colonnes] * lignes) # =================================== # Fonction pour saisir un entier n # =================================== def saisie(): n = int(input('donner n telque 3<=n<=10: ')) # Tant que n n’est pas dans l’intervalle demandé, on redemande while (n < 3) or (n > 10): n = int(input('donner n telque 3<=n<=10: ')) return n # ========================================= # Remplir la matrice T avec les coordonnées # ========================================= def remplir_matrice_T(t, n): code_ASCII = 65 # 65 correspond à 'A' for i in range(n): # Saisie de l'abscisse du point A, B, C, ... t[0][i] = int(input('donner Abscisse du point ' + chr(code_ASCII + i) + ': ')) # Saisie de l'ordonnée t[1][i] = int(input('donner Ordonnee du point ' + chr(code_ASCII + i) + ': ')) # ========================================= # Affichage de la matrice T # ========================================= def afficher_matrice_T(t, n): print('****** Matrice T ******') code_ASCII = 65 # Affichage des noms des points for i in range(n): print(chr(code_ASCII + i), end=' ') print() # Affichage des abscisses for i in range(n): print(t[0][i], end=' ') print() # Affichage des ordonnées for i in range(n): print(t[1][i], end=' ') print() # ========================================= # Calcul de la distance entre deux points # ========================================= def calcul_distance(x1, x2, y1, y2): # Distance euclidienne : √((x2 − x1)² + (y2 − y1)²) return sqrt((x2 - x1) * (x2 - x1) + (y2 - y1) * (y2 - y1)) # ========================================= # Construction de la matrice des distances M # ========================================= def remplir_matrice_M(m, n): for i in range(n): for j in range(n): # Distance entre le point i et le point j formatée sur 1 chiffre après la virgule m[i][j] = "{:.1f}".format(calcul_distance(t[0][i], t[0][j], t[1][i], t[1][j])) # ========================================= # Affichage de la matrice M # ========================================= def afficher_matrice_M(m, n): print('****** Matrice M ******') code_ASCII = 65 # Première ligne : noms des points print(end=' ') for i in range(n): print(chr(code_ASCII + i), end=' ') print() # Lignes suivantes : index + valeurs for i in range(n): print(chr(code_ASCII + i), end=' ') for j in range(n): print(m[i][j], end=' ') print() # ========================================= # Saisie d’un point dont on cherche le voisin le plus proche # ========================================= def saisie_point(n): point = input('donner le nom du point entre A et ' + chr(65 + n) + ' : ') # Vérification de validité : doit être une lettre entre A et A+n while (ord(point) < 65) or (ord(point) > 65 + n): point = input('donner le nom du point entre A et ' + chr(65 + n) + ' : ') return point # ========================================= # Trouver le point le plus proche d’un point donné # ========================================= def point_plus_proche(point, m, n): indice_proche = 0 # Avancer jusqu'à trouver une distance différente de 0 (éviter A → A = 0) while m[indice_proche][ord(point) - 65] == 0: indice_proche += 1 # Recherche de la distance strictement minimale for i in range(1, n): if (m[i][ord(point) - 65] != 0) and (m[i][ord(point) - 65] < m[indice_proche][ord(point) - 65]): indice_proche = i # Retourne le nom du point correspondant return chr(indice_proche + 65) # ============================ # PROGRAMME PRINCIPAL # ============================ n = saisie() # Saisie du nombre de points remplir_matrice_T(t, n) # Saisie des coordonnées afficher_matrice_T(t, n) # Affichage de T remplir_matrice_M(m, n) # Calcul des distances afficher_matrice_M(m, n) # Affichage de M point = saisie_point(n) # Choix du point print('Le premier point le plus proche de ' + point + ' est: ' + point_plus_proche(point, m, n)) |
0 commentaire
laisser un commentaire
Passion de robotique
Tutoriels récents
Atelier robotique
Tutoriels populaires
Construction des robots
Tutoriels plus commentés
Bras robotique
Categories
Maison intelligente
