Matrice – Bac théorique – Section informatique – 2022

Sujet (Algo et programmation - Bac 2022)
En mathématique, une matrice carrée M de dimension n x n est dite stochastique (ou encore matrice de Markov) lorsque chaque élément de la matrice est un réel de l’intervalle [0, 1] et la somme des éléments de chaque ligne est égale à 1.
Un tableau T de n réels est dit stable pour une matrice stochastique M lorsque le tableau P résultat du produit de T et M vérifie P = T (T x M = P = T), sachant que le tableau P est obtenu comme suit :
𝑃[j] = ∑ 𝑀[𝑖, j] * 𝑇[𝑖] 𝑎𝑣𝑒𝑐 0 ≤ j ≤ 𝑛 − 1
Exemple : Pour la matrice carrée M de dimension 3x3 et le tableau T de 3 éléments suivants :
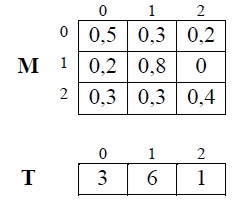
M est une matrice stochastique puisque les éléments de M sont tous des réels de l’intervalle [0,1] et la somme des éléments de chaque ligne est égale à 1.
En effet :
La somme des éléments de la 1ère ligne est égale à M[0,0] + M[0,1] + M[0,2] = 0,5+0,3+0,2 = 1 La somme des éléments de la 2ème ligne est égale à M[1,0] + M[1,1] + M[1,2] = 0,2+0,8+0 = 1 La somme des éléments de la 3ème ligne est égale à M[2,0] + M[2,1] + M[2,2] = 0,3+0,3+0,4 = 1
P, le tableau résultat du produit M x T est :
En effet :
P[0] = M[0,0]*T[0] + M[1,0]*T[1] + M[2,0]*T[2] = 0,5*3+0,2*6+0,3*1 = 3 qui est égal à T[0]
P[1] = M[0,1]*T[0] + M[1,1]*T[1] + M[2,1]*T[2] = 0,3*3+0,8*6+0,3*1 = 6 qui est égal à T[1]
P[2] = M[0,2]*T[0] + M[1,2]*T[1] + M[2,2]*T[2] = 0,2*3+0*6+0,4*1 = 1 qui est égal à T[2]
T est dit stable pour M car M est stochastique et le produit P de T et M est égal à T.
Travail demandé :
1. Analyser le problème en le décomposant en modules.
2. Ecrire les algorithmes des modules envisagés.
Solution Algorithmique
Dans cet algorithme, On va utiliser quatre fonctions et trois procédures :
- la fonction saisie_n()
- la fonction saisie_elt()
- la fonction stochastique()
- la procédure remplir_matrice()
- la procédure remplir_tableau()
- la procédure produit_matrice_tableau()
- la fonction test_stable()
Algorithme du programme Principal
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
Algorithme matrice_stable Debut n <- saisie_n() # Saisie de la taille remplir_matrice(m, n) # Remplissage de la matrice M remplir_tableau(t, n) # Remplissage du tableau T produit_matrice_tableau(m, t, p, n) # Calcul du produit # Test de stabilité Si test_stable(t, p, n) alors Ecrire('Le tableau T est stable') else: Ecrire('Le tableau T est non stable') Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
| m | matrice |
| t | tableau |
| p | tableau |
La fonction saisie_n()
La fonction saisie_n() sert à demander à l’utilisateur de saisir un entier valide n supérieur ou égal à 2, puis à vérifier cette saisie avant de la retourner.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
Fonction saisie_n():entier # Demande à l'utilisateur de saisir un entier n Ecrire('donner n >= 2 : ') Lire(n) # Vérification de la validité de la saisie # Tant que n est inférieur à 2, on redemande la saisie Tant que Non (n >= 2) faire Ecrire('donner n >= 2 : ') Lire(n) Fin tant que # Retourne la valeur valide de n retourner n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La fonction saisie_elt()
Cette fonction permet de saisir un nombre réel compris entre 0 et 1, en assurant la validation de la saisie.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
Fonction saisie_n):entier # Saisie d’un entier compris entre 0 et 1 Ecrire('donner un entier n telque 0<=n<=1 :') Lire(n) # Vérification de la validité de la saisie Tant que Non (0<=n<=1) faire Ecrire('donner un entier n telque 0<=n<=1 :') Lire(n) Fin tant que # Retourne la valeur valide de n retourner n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La fonction stochastique
La fonction stochastique vérifie si la matrice m est stochastique, c’est-à-dire si la somme des éléments de chaque ligne est égale à 1.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
Fonction stochastique(m:matrice, n:entier):booleen i <- 0 somme <- 1 # Parcours des lignes de la matrice Tant que (i <= n - 1) et (somme = 1) faire somme <- 0 Pour j de 0 à n-1 faire somme <- somme + m[i][j] Fin pour i <- i + 1 Ecrire(somme) # Affichage de la somme de chaque ligne Fin tant que # Retourne Vrai si toutes les lignes ont une somme égale à 1 return somme = 1 Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| somme | entier |
| j | entier |
La procédure remplir_matrice
Cette procédure permet de remplir une matrice carrée m de taille n × n avec des valeurs saisies par l’utilisateur, tout en garantissant que la matrice est stochastique.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
Procedure remplir_matrice(m:matrice, n:entier) test <- Faux # Répéter la saisie tant que la matrice n’est pas stochastique Tant que (test = Faux) faire Ecrire('Saisir une matrice M stochastique') Pour i de 0 à n-1 faire Pour j de 0 à n-1 faire m[i][j] <- saisie_elt() Fin pour Fin pour # Vérification de la propriété stochastique Si (stochastique(m, n) = Vrai) alors test = Vrai Fin si Fin tant que Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| j | entier |
| test | booleen |
La procédure remplir_tableau
Cette procédure permet de remplir le tableau T de taille n avec des valeurs saisies par l’utilisateur.
|
1 2 3 4 5 6 7 |
Procédure remplir_tableau(t:tableau, n:entier) Ecrire('remplir un tableau T') Pour i de 0 à n-1 faire Ecrire('Donner un elt : ') Lire(t[i]) Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
La procédure produit_matrice_tableau
Cette procédure permet de calculer le produit de la matrice M par le tableau T et de stocker le résultat dans le tableau P.
|
1 2 3 4 5 6 7 8 9 |
Procédure produit_matrice_tableau(m:matrice, t:tableau, p:tableau, n:entier) Pour j de 0 à n-1 faire produit <- 1 Pour i de 0 à n-1 faire produit <- produit * m[i][j] * t[i] Fin pour p[j] <- produit Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| j | entier |
| produit | entier |
La procédure test_stable
Cette fonction permet de tester si le tableau T est stable, c’est-à-dire s’il est identique au tableau P.
|
1 2 3 4 5 6 7 8 9 |
Procedure test_stable(t:tableau, p:tableau, n:entier) i <- 0 # Comparaison élément par élément Tant que (i < n - 1) et (t[i] = p[i]) faire i <- i + 1 Fin tant que retourner (t[i] = p[i]) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 |
from numpy import * # -------------------------------------------------- # Définition des dimensions maximales de la matrice # -------------------------------------------------- lignes = 50 # Nombre maximal de lignes colonnes = 50 # Nombre maximal de colonnes # -------------------------------------------------- # Création des structures de données # -------------------------------------------------- # Matrice M de taille 50x50 initialisée à 0 m = array([[float()] * colonnes] * lignes) # Tableau T de taille 50 t = array([float()] * 50) # Tableau P de taille 50 (résultat du produit) p = array([float()] * 50) # -------------------------------------------------- # Fonction de saisie de la taille de la matrice # -------------------------------------------------- def saisie_n(): # Saisie d’un entier n (taille de la matrice carrée) n = int(input('donner la taille de la matrice carré >=2 : ')) # Vérification que n est supérieur ou égal à 2 while (n < 2): n = int(input('donner la taille de la matrice carré >=2 : ')) # Retourne une valeur valide return n # -------------------------------------------------- # Fonction de saisie d’un élément de la matrice # -------------------------------------------------- def saisie_elt(): # Saisie d’un réel compris entre 0 et 1 n = float(input('donner un entier n telque 0<=n<=1 : ')) # Vérification de l’intervalle while not (0 <= n <= 1): n = float(input('donner un entier n telque 0<=n<=1 : ')) # Retourne la valeur valide return n # -------------------------------------------------- # Fonction qui vérifie si une matrice est stochastique # (la somme des éléments de chaque ligne est égale à 1) # -------------------------------------------------- def stochastique(m, n): i = 0 somme = 1 # Parcours des lignes de la matrice while (i <= n - 1) and (somme == 1): somme = 0 for j in range(n): somme = somme + m[i][j] i = i + 1 print(somme) # Affichage de la somme de chaque ligne # Retourne True si toutes les lignes ont une somme égale à 1 return somme == 1 # -------------------------------------------------- # Procédure de remplissage de la matrice stochastique # -------------------------------------------------- def remplir_matrice(m, n): test = False # Répéter la saisie tant que la matrice n’est pas stochastique while (test == False): print('Saisir une matrice M stochastique') for i in range(n): for j in range(n): m[i][j] = saisie_elt() # Vérification de la propriété stochastique if (stochastique(m, n) == True): test = True # -------------------------------------------------- # Procédure de remplissage du tableau T # -------------------------------------------------- def remplir_tableau(t, n): print('remplir un tableau T') for i in range(n): t[i] = float(input('Donner un elt : ')) # -------------------------------------------------- # Procédure qui calcule le produit de la matrice M # par le tableau T et stocke le résultat dans P # -------------------------------------------------- def produit_matrice_tableau(m, t, p, n): for j in range(n): produit = 1 for i in range(n): produit = produit * m[i][j] * t[i] p[j] = produit # -------------------------------------------------- # Fonction qui teste la stabilité du tableau T # (T est stable si T = P) # -------------------------------------------------- def test_stable(t, p, n): i = 0 # Comparaison élément par élément while (i < n - 1) and (t[i] == p[i]): i = i + 1 return (t[i] == p[i]) # -------------------------------------------------- # Programme principal # -------------------------------------------------- n = saisie_n() # Saisie de la taille remplir_matrice(m, n) # Remplissage de la matrice M remplir_tableau(t, n) # Remplissage du tableau T produit_matrice_tableau(m, t, p, n) # Calcul du produit # Test de stabilité if test_stable(t, p, n): print('Le tableau T est stable') else: print('Le tableau T est non stable') |
Exécution du programme

0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés
























