Nombre Rigolo – Bac pratique – Section informatique – 2011

Sujet (Algo et programmation - Bac 2011)
Un nombre Nb et dit rigolo si la somme de ses chiffres est égale à la somme de tous les chiffres de ses facteurs premiers.
Exemple 1 :
Si Nb = 690, alors Nb est un nombre rigolo. En effet :
■ La somme des chiffres de 690 est : 6 + 9 + 0 = 15
■ Les facteurs premiers de 690 sont : 2, 3, 5 et 23
■ La somme des chiffres des facteurs premiers de 690 est : 2 + 3 + 5 + 2 + 3 = 15
Exemple 2 :
Si Nb =120, alors Nb n'est pas un nombre rigolo. En effet :
■ La somme des chiffres de 120 est : 1 + 2 + 0 = 3
■ Les facteurs premiers de 120 sont : 2, 2, 2, 3 et 5
La somme des chiffres des facteurs premiers de 120 est :.2 + 2 + 2 + 3 + 5 = 10
Travail demandé :
Ecrire un programme Pascal qui permet de :
1- Chercher tous les nombres rigolos dans l'intervalle [M, N] avec M et N, 2 entiers saisis tels que :
![]()
2- Stocker les résultats trouvés dans un fichier texte nommé « resultat.txt » tel que : Chaque ligne du fichier contient un nombre rigolo suivi du symbole « = », suivi de ses facteurs premiers séparés par une étoile (« * », symbolisant la multiplication). Pour l'exemple précédent, le nombre 690 sera stocké de la manière suivante : 690=2*3*5*23
3- Afficher le contenu du fichier « resultat.txt ».
Si ce fichier est vide, le programme affichera le message « Il n'y a aucun nombre rigolo ».
Solution Algorithmique
Dans cet algorithme, On va utiliser cinq fonctions et une procédure:
- la fonction saisie()
- la fonction test_premier()
- la fonction facteur_premiers()
- la fonction insertion_etoiles_facteurs_premiers()
- la fonction somme_chiffres()
- la procédure remplir_fichier_resultat()
Algorithme du programme Principal
|
1 2 3 4 5 6 7 8 9 |
Algorithme Nombre_Rigolo Debut # Saisie de la borne inférieure m m = saisie(100, 1000) # Saisie de la borne supérieure n (n > m) n = saisie(m, 1000) # Recherche des nombres rigolos et écriture des résultats remplir_fichier_resultat(m, n) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| m | entier |
| n | entier |
La fonction saisie
Cette procédure permet de saisir un entier compris strictement entre deux bornes inf et sup, en contrôlant la validité de la saisie.
Plus précisément :
il demande à l’utilisateur d’entrer un entier n tel que inf < n < sup ; si la valeur saisie n’appartient pas à cet intervalle, le programme redemande la saisie jusqu’à obtenir une valeur correcte ; une fois la saisie valide, la fonction retourne l’entier n.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
Fonction saisie(inf:entier, sup:entier):entier # Première saisie de l'entier Ecrire('donner un entier tel que ' + inf + '< n < ' + sup + ' : ') Lire(n) # Tant que n n'est pas dans l'intervalle demandé, # on redemande la saisie Tant que (n <= inf) ou (n >= sup) faire Ecrire('donner un entier tel que ' + inf + '< n < ' + sup + ' : ') Lire(n) Fin tant que # Retourne la valeur correcte saisie retourner n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | chaîne |
La fonction test_premier
Ce programme permet de tester si un entier n est un nombre premier.
Fonctionnement :
Il cherche un diviseur de n à partir de 2.
Tant que n n’est pas divisible par i et que i ne dépasse pas n // 2, il incrémente i
Si aucun diviseur n’est trouvé, alors n est premier.
|
1 2 3 4 5 6 7 8 9 10 |
Fonction test_premier(n:entier): booleen i <- 2 # Recherche d’un diviseur de n # On s’arrête si i divise n ou si i dépasse n//2 Tant que (n mod i != 0) ou (i <= n div 2): i <- i + 1 Fin tant que # Si aucun diviseur n’a été trouvé, n est premier retourner n mod i != 0 Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
La fonction facteur_premiers
Cette fonction permet de déterminer la décomposition en facteurs premiers d’un entier n et de la retourner sous forme d’une chaîne de caractères contenant uniquement les facteurs premiers trouvés, sans séparateur.
Elle procède en testant successivement les diviseurs à partir de 2, divise n chaque fois qu’un facteur premier est trouvé, et ajoute ce facteur à la chaîne résultat jusqu’à ce que n devienne égal à 1.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
Fonction facteur_premiers(n:entier): chaine i <- 2 # Premier diviseur possible ch <- '' # Chaîne pour stocker les facteurs # Décomposition de n en facteurs premiers Tant que (n > 1) faire Si (n mod i = 0) alors ch <- ch + Convch(i) # Ajouter le facteur trouvé n <- n / i # Diviser n par ce facteur Sinon i <- i + 1 # Tester le diviseur suivant Fin si Fin tant que # Retourner la chaîne contenant les facteurs return ch Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| ch | chaîne |
La fonction insertion_etoiles_facteurs_premiers
Cette fonction permet de calculer la décomposition en facteurs premiers d’un entier n et de la retourner sous forme d’une chaîne de caractères, dans laquelle les facteurs premiers sont séparés par des étoiles (*).
Elle teste successivement les diviseurs à partir de 2, divise n chaque fois qu’un facteur premier est trouvé, ajoute ce facteur suivi d’une étoile à la chaîne résultat, puis supprime la dernière étoile avant de retourner le résultat final.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
Fonction insertion_etoiles_facteurs_premiers(n:entier): chaine i <- 2 # Premier diviseur possible ch <- '' # Chaîne pour stocker les facteurs # Décomposition de n en facteurs premiers Tant que (n > 1) faire Si (n mod i = 0) alors ch <- ch + Convch(i) + '*' # Ajouter le facteur suivi de * n <- n / i # Diviser n par ce facteur Sinon i <- i + 1 # Tester le diviseur suivant Fin si Fin tant que # Supprimer la dernière étoile avant de retourner la chaîne retourner Sous_chaine(ch,0,long(ch)-2) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| ch | chaîne |
La fonction somme_chiffres
Cette fonction permet de calculer et retourner la somme des chiffres d’un nombre représenté sous forme de chaîne de caractères.
Elle parcourt chaque caractère de la chaîne ch, le convertit en entier, puis l’ajoute à une variable somme.
|
1 2 3 4 5 6 7 |
Fonction somme_chiffres(ch:chaine): chaine somme <- 0 Pour i de 0 à long(ch)-1 faire somme <- somme + int(ch[i]) Fin pour retourner somme Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| somme | entier |
La procédure remplir_fichier_resultat
Cette procédure cherche tous les nombres « rigolos » compris entre m et n et enregistre les résultats dans un fichier texte tout en les affichant à l’écran.
Cette procédure :
1- ouvre le fichier resultat.txt en mode écriture.
2- parcourt tous les entiers entre m et n.
Pour chaque nombre i, teste s’il est rigolo avec les critères ci-dessus.
Si i est rigolo :
Affiche i et sa décomposition en facteurs premiers (avec *) à l’écran.
Écrit cette information dans le fichier.
Si aucun nombre rigolo n’est trouvé, affiche un message correspondant.
3- ferme le fichier.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
Procédure remplir_fichier_resultat(m:entier,n:entier) # Ouverture du fichier en mode écriture Ouvrir(f , "resultat.txt", "w") test_vide <- Vrai # Indique s'il existe au moins un nombre rigolo # Parcours de tous les entiers entre m et n Pour i de m à n + 1 faire # Vérifier si i n'est pas premier et si la somme de ses chiffres # est égale à la somme des chiffres de sa décomposition Si non(test_premier(i)) et (somme_chiffres(Convch(i)) = somme_chiffres(facteur_premiers(i))): test_vide <- Faux # Affichage du résultat à l’écran Ecrire(i + ' = ' + insertion_etoiles_facteurs_premiers(i)) # Écriture du résultat dans le fichier Ecrire(f,i + ' = ' + insertion_etoiles_facteurs_premiers(i) + '\n') Fin si Fin pour # Si aucun nombre rigolo n’a été trouvé Si test_vide alors Ecrire("Il n'y a aucun nombre rigolo.") Fin si # Fermeture du fichier Fermer(f) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| f | fichier |
| i | entier |
| test_vide | booléen |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 |
# -------------------------------------------------- # Fonction saisie # Permet de saisir un entier strictement compris # entre deux bornes inf et sup # -------------------------------------------------- def saisie(inf, sup): # Saisie initiale de l'entier n = int(input('donner un entier n tel que ' + str(inf) + '< n < ' + str(sup) + ' : ')) # Répéter la saisie tant que n n'est pas dans l'intervalle demandé while (n <= inf) or (n >= sup): n = int(input('donner un entier n tel que ' + str(inf) + '< n < ' + str(sup) + ' : ')) # Retourner la valeur valide saisie return n # -------------------------------------------------- # Fonction test_premier # Teste si un entier n est premier # Retourne True si n est premier, False sinon # -------------------------------------------------- def test_premier(n): i = 2 # Premier diviseur possible # Recherche d’un diviseur de n # La boucle s'arrête si i divise n # ou si i dépasse la moitié de n while (n % i != 0) and (i <= n // 2): i = i + 1 # Si aucun diviseur n’a été trouvé, n est premier return n % i != 0 # -------------------------------------------------- # Fonction facteur_premiers # Retourne la décomposition en facteurs premiers # d’un entier n sous forme de chaîne de caractères # -------------------------------------------------- def facteur_premiers(n): i = 2 # Premier diviseur possible ch = '' # Chaîne pour stocker les facteurs # Décomposition de n en facteurs premiers while (n > 1): if (n % i == 0): ch = ch + str(i) # Ajouter le facteur trouvé n = n / i # Diviser n par ce facteur else: i = i + 1 # Tester le diviseur suivant # Retourner la chaîne contenant les facteurs return ch # -------------------------------------------------- # Fonction insertion_etoiles_facteurs_premiers # Retourne la décomposition en facteurs premiers # avec des étoiles (*) entre les facteurs # -------------------------------------------------- def insertion_etoiles_facteurs_premiers(n): i = 2 ch = '' # Décomposition en facteurs premiers while (n > 1): if (n % i == 0): ch = ch + str(i) + '*' # Ajouter le facteur suivi de * n = n / i else: i = i + 1 # Supprimer la dernière étoile avant de retourner la chaîne return ch[0:len(ch) - 1] # -------------------------------------------------- # Fonction somme_chiffres # Calcule et retourne la somme des chiffres # d'une chaîne représentant un nombre # -------------------------------------------------- def somme_chiffres(ch): somme = 0 for i in range(len(ch)): somme = somme + int(ch[i]) return somme # -------------------------------------------------- # Fonction remplir_fichier_resultat # Recherche les nombres "rigolos" entre m et n # Affiche les résultats et les écrit dans un fichier # -------------------------------------------------- def remplir_fichier_resultat(m, n): # Ouverture du fichier résultat en mode écriture f = open("resultat.txt", "w") test_vide = True # Indique s'il existe au moins un nombre rigolo # Parcours de tous les entiers entre m et n for i in range(m, n + 1): # Vérifier si i n'est pas premier et si la somme de ses chiffres # est égale à la somme des chiffres de sa décomposition if not(test_premier(i)) and (somme_chiffres(str(i)) == somme_chiffres(facteur_premiers(i))): test_vide = False # Affichage du résultat à l’écran print(str(i) + ' = ' + insertion_etoiles_facteurs_premiers(i)) # Écriture du résultat dans le fichier f.write(str(i) + ' = ' + insertion_etoiles_facteurs_premiers(i) + '\n') # Message affiché si aucun nombre rigolo n’a été trouvé if test_vide: print("Il n'y a aucun nombre de rigolo") # Fermeture du fichier f.close() # -------------------------------------------------- # Programme principal # -------------------------------------------------- # Saisie de la borne inférieure m m = saisie(100, 1000) # Saisie de la borne supérieure n (n > m) n = saisie(m, 1000) # Recherche des nombres rigolos et écriture des résultats remplir_fichier_resultat(m, n) |
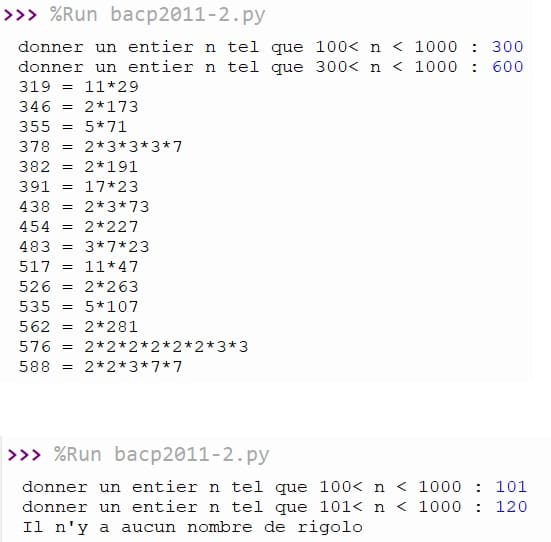
Exécution du programme
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés