Problème matrice – Bac théorique – Section informatique – 2010
Sujet (Algo et programmation - Bac 2010)
On se propose d'écrire un programme permettant de :
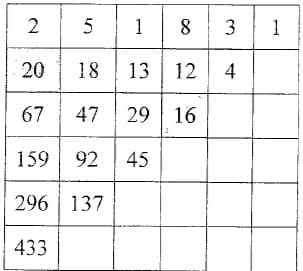
M [1, 0] = 2 + 5 +1 + 8 + 3 + 1 = 20 , M [2, 3] = 12 + 4 = 16
2) Chaque ligne du fichier diagonal.txt contiendra les éléments de M se trouvant sur une diagonale droite, en commençant par celle à gauche et de haut en bas, de telle sorte que :
- La ligne N°1 du fichier contient M [0, 0] c'est à dire 2
- La ligne N°2 du fichier contient M [0, 1] suivi de M [1, 0] c'est-à-dire 520
- La ligne N°3 du fichier contient M [0, 2] suivi de M [1, 1] suivi de M [2, 0] c'est-à-dire 11867
Pour l'exemple précédant, le contenu du fichier diagonal.txt sera comme suit :
7
520
11867
81347159
3122992296
141645137433
et les lignes qui seront affichées sont :
11867
81347159
3122992296
141645137433
En effet :
- La ligne numéro 0 n'est pas affichée car elle ne contient qu'un seul chiffre.
- La ligne numéro 1 n'est pas affichée car on ne trouve que 3 chiffres distincts.
- Les lignes numéro 2, 3, 4 et 5 seront affichées car elles contiennent chacune au moins 4 chiffres distincts.
Travail demandé
1. Analyser le problème en le décomposant en modules et déduire l'algorithme du programme principal qui permet de réaliser le traitement décrit précédemment.
2. Analyser chacun des modules envisagés précédemment et en déduire les algorithmes correspondants.
Solution Algorithmique
Dans cet algorithme, On va utiliser deux fonctions et quatre procédures :
- la fonction saisie()
- la procédure remplir_matrice()
- la procédure afficher_matrice()
- la fonction test_different()
- la procédure remplir_fichier_diagonal()
- la procédure afficher_fichier()
Algorithme du programme Principal
|
1 2 3 4 5 6 7 8 9 10 11 |
Algorithme matrice_diagonale Debut # Saisie de la dimension de la matrice n <- saisie() # Remplissage de la matrice remplir_matrice(m, n) # Affichage de la matrice afficher_matrice(m, n) # Traitement des diagonales et sauvegarde dans un fichier remplir_fichier_diagonal(m, n) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
| m | matrice |
La fonction saisie_nbr_chaines
Cette fonction demande à l’utilisateur de saisir un entier compris entre 2 et 10.
Tant que la valeur saisie n’est pas dans cet intervalle, la fonction redemande un nombre.
Elle garantit donc que le nombre retourné sera toujours un entier valide entre 2 et 10.
|
1 2 3 4 5 6 7 8 9 10 |
Fonction saisie_nbr_chaines(): entier Ecrire('donner n tel que 2<=n<=10: ') lire (n) # Tant que la valeur n'est pas dans l’intervalle demandé, on redemande Tant que (n < 2) ou (n > 10) faire Ecrire('donner n tel que 2<=n<=10: ') lire (n) Fin tant que retourner n fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La fonction saisie
Ce programme permet de saisir un entier n compris entre 5 et 10 inclus, en contrôlant la validité de la saisie.
Il redemande la valeur tant que l’utilisateur entre un nombre en dehors de l’intervalle [5, 10], puis retourne la valeur correcte une fois la condition respectée.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
Fonction saisie(): entier # Saisie d’un entier n Ecrire('donner n telque 5<=n<=10: ') Lire(n) # Vérification de l’intervalle Tant que (n < 5) ou (n > 10) faire Ecrire('donner n telque 5<=n<=10: ') Lire(n) Fin tant que # Retourner la valeur valide return n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La procédure remplir_matrice
Cette procédure permet de remplir une matrice m de dimension n × n de la manière suivante :
- La première ligne de la matrice est remplie par des nombres aléatoires compris entre 1 et 9.
Chaque élément des lignes suivantes est calculé comme la somme des éléments de la ligne précédente, depuis une colonne donnée jusqu’à la dernière colonne.
La matrice obtenue a une forme triangulaire, car seules les premières colonnes de chaque ligne sont remplies.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
Procédure remplir_matrice(m, n) # Remplissage de la première ligne avec des valeurs aléatoires entre 1 et 9 Pour j de 0 à n-1 faire m[0][j] <- Alea(1, 9) Fin pour # Remplissage des autres lignes Pour i de 1 à n-1 faire Pour j de 0 à n-i-1 faire somme <- 0 # Calcul de la somme des éléments de la ligne précédente # à partir de la colonne j jusqu'à la fin Pour k de j à n-1 faire somme <- somme + m[i - 1][k] Finpour # Affectation de la somme à la case m[i][j] m[i][j] <- somme Fin pour Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| j | entier |
| k | entier |
| somme | entier |
La fonction recherche_base
Cette fonction détermine la plus petite base possible dans laquelle la chaîne ch peut être interprétée.
Elle cherche le caractère le plus grand dans la chaîne ch (par exemple : dans "A3F2", le plus grand caractère est 'F').
Selon ce caractère maximal :
1- S’il s’agit d’une lettre entre A et F, elle calcule sa valeur :
A → 10
B → 11
…
F → 15
Puis elle retourne valeur + 1, donc la base minimale.
2- S’il s’agit d’un chiffre, elle retourne (chiffre + 1).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
Fonction recherche_base(ch:chaine):entier max_chiffre <- ch[0] # Recherche du plus grand caractère Pour i de 1 à long(ch)-1 faire Si max_chiffre < ch[i] alors max_chiffre <- ch[i] Finsi Fin pour # Si le caractère est une lettre A..F Si 'A' <= max_chiffre <= 'F' alors retourner ord(max_chiffre) - 54 # Convertir A→10, B→11 ... F→15 Sinon retourner Valeur(max_chiffre) + 1 # Sinon base = chiffre + 1 Finsi Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| max_chiffre | entier |
La fonction exposant
Cette fonction calcule la puissance d’un nombre : c’est-à-dire n multiplié par lui-même e fois.
|
1 2 3 4 5 6 7 |
Fonction exposant(n:entier;e:entier):entier p <- 1 Pour i de 0 à e-1 faire p <- p * n finpour retourner p Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| p | entier |
La fonction conversion_decimale
Cette fonction convertit un nombre écrit dans une base quelconque (≤ 16) en base 10.
La chaîne ch contient un nombre composé :
- de chiffres 0 à 9 ou de lettres A à F (pour les valeurs 10 à 15)
- de la base dans laquelle ce nombre est écrit.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
Fonction conversion_decimale(ch:chaine, base:entier):entier nombre <- 0 Pour i de 0 à long(ch)-1 faire # Conversion du caractère en valeur numérique Si 'A' <= ch[i] <= 'F' alors x <- ord(ch[i]) - 55 # A=10, B=11, ..., F=15 Sinon x <- int(ch[i]) finsi # Ajout contribution du chiffre : valeur * base^(position) nombre = nombre + x * exposant(base, long(ch) - i - 1) finpour retourner nombre fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| nombre | entier |
| i | entier |
La procédure remplir_fichiers
Cette procédure remplit deux fichiers à partir de chaînes saisies par l’utilisateur.
nb_base.dat : ce fichier contient les chaînes originales, telles que saisies par l’utilisateur.
nombre.txt : ce fichier contient leurs conversions en base 10, accompagnées de la base minimale utilisée.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
Procédure remplir_fichiers(n:entier) Ouvrir(f_nbbase , "nb_base.dat", "w") # Fichier des chaînes originales Ouvrir(f_nombre , "nombre.txt", "w") # Fichier des conversions Pour i de 0 à n-1 faire ch <- saisie_chaine() # Saisie d'une chaîne Ecrire(f_nbbase ,ch + '\n') # Sauvegarde dans le fichier base <- recherche_base(ch) # Calcul de la base minimale nombre <- conversion_decimale(ch, base) # Conversion en base 10 # Exemple d’écriture : (A3)11 = (113)10 Ecrire(f_nombre,'(' + ch + ')' + base + '= (' + nombre + ')10\n') Fin pour Fermer(f_nbbase) Fermer(f_nombre) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| f_nbbase | fichier |
| f_nombre | fichier |
| i | entier |
| ch | chaîne |
| base | entier |
| nombre | entier |
La procédure afficher_fichier
Cette procédure sert à afficher le contenu d’un fichier texte, ligne par ligne.
|
1 2 3 4 5 6 7 8 9 |
Procédure afficher_fichier(nom_fichier:chaine) Ecrire('*****' + nom_fichier + '****') Ouvrir(f , nom_fichier , "r") Lire_lignes (f , ch) # Lecture des lignes dans une liste Pour nombre dans ch faire Ecrire(nombre) # Affichage sans le retour à la ligne final Faire Fermer(f) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| f | fichier |
| ch | chaîne |
| nombre | chaîne |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 |
# Fonction qui permet de saisir un entier n entre 2 et 10 def saisie_nbr_chaines() : n = int(input("donner un entier entre 2 et 10: ")) # Répéter tant que n n’est pas dans l’intervalle while (n < 2) or (n > 10) : n = int(input("donner un entier entre 2 et 10: ")) return n # Vérifie qu'une chaîne est valide : # - longueur entre 1 et 5 # - composée uniquement de chiffres 0..9 ou lettres A..F def verif_chaine(ch): if 1 <= len(ch) <= 5: # Vérification de la longueur i = 0 # Vérifier tous les caractères sauf le dernier while (i < len(ch) - 1) and (('A' <= ch[i] <= 'F') or ('0' <= ch[i] <= '9')): i = i + 1 # Vérifier le dernier caractère return ('A' <= ch[i] <= 'F') or ('0' <= ch[i] <= '9') else: return False # Saisie d'une chaîne valide formée de chiffres ou de A..F def saisie_chaine(): ch = input("donner une chaine au 5 caractéres max et formée des chiffres ou A..F: ") # Tant que la chaîne est invalide on redemande while verif_chaine(ch) == False : ch = input("donner une chaine au 5 caractéres max et formée des chiffres ou A..F: ") return ch # Détermination automatique de la base minimum : # La base est le chiffre ou la lettre la plus grande + 1 # Exemple : 'A3' → plus grand = 'A' → base = 10 + 1 = 11 def recherche_base(ch): max_chiffre = ch[0] # Recherche du plus grand caractère for i in range(1, len(ch)): if max_chiffre < ch[i]: max_chiffre = ch[i] # Si le caractère est une lettre A..F if 'A' <= max_chiffre <= 'F': return ord(max_chiffre) - 54 # Convertir A→10, B→11 ... F→15 else: return int(max_chiffre) + 1 # Sinon base = chiffre + 1 # Calcul de n exposant e (n^e) def exposant(n, e): p = 1 for i in range(e): p = p * n return p # Convertit la chaîne ch (écrite dans une base donnée) en base 10 def conversion_decimale(ch, base): nombre = 0 for i in range(len(ch)): # Conversion du caractère en valeur numérique if 'A' <= ch[i] <= 'F': x = ord(ch[i]) - 55 # A=10, B=11, ..., F=15 else: x = int(ch[i]) # Ajout contribution du chiffre : valeur * base^(position) nombre = nombre + x * exposant(base, len(ch) - i - 1) return nombre # Remplit deux fichiers : # - nb_base.dat : contient les chaînes saisies # - nombre.txt : contient leur conversion en base 10 def remplir_fichiers(n): f_nbbase = open("nb_base.dat", "w") # Fichier des chaînes originales f_nombre = open("nombre.txt", "w") # Fichier des conversions for i in range(n): ch = saisie_chaine() # Saisie d'une chaîne f_nbbase.write(ch + '\n') # Sauvegarde dans le fichier base = recherche_base(ch) # Calcul de la base minimale nombre = conversion_decimale(ch, base) # Conversion en base 10 # Exemple d’écriture : (A3)11 = (113)10 f_nombre.write('(' + ch + ')' + str(base) + '= (' + str(nombre) + ')10\n') f_nbbase.close() f_nombre.close() # Affiche le contenu d'un fichier texte ligne par ligne def afficher_fichier(nom_fichier): print('*****' + nom_fichier + '****') f = open(nom_fichier, "r") ch = f.readlines() # Lecture des lignes dans une liste for nombre in ch: print(nombre.rstrip('\n')) # Affichage sans le retour à la ligne final f.close() # Programme principal n = saisie_nbr_chaines() # Saisie du nombre de chaînes à traiter remplir_fichiers(n) # Génération des fichiers afficher_fichier("nb_base.dat") # Affichage du fichier 1 afficher_fichier("nombre.txt") # Affichage du fichier 2 |
Exécution du programme
0 commentaire
laisser un commentaire
Passion de robotique
Tutoriels récents
Atelier robotique
Tutoriels populaires
Construction des robots
Tutoriels plus commentés
Bras robotique
Categories
Maison intelligente
