Suite – Bac pratique – Section informatique- 2009

Sujet (Algo et programmation - Bac 2009)
Soit Uo un nombre entier naturel de quatre chiffres. On forme a l'aide des quatre chiffres de U0, le plus grand entier nature! Max et le plus petit entier nature! min.
Leur différence (Max - min) donne le nombre U1
On refait le même travail pour U1 et on obtient ainsi une suite. Cette suite est stationnaire c'est-a-dire qu'elle devient constante a partir d'un certain rang.
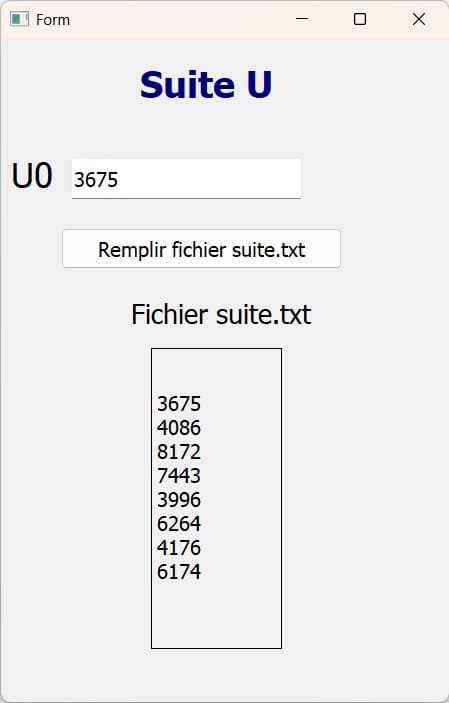
Ecrire un programme en Python qui calcule et affiche les termes de la suite U jusqu'à ce qu'elle devienne constante. Le premier terme Uo est un entier donne de quatre chiffres. En même temps, les termes calcules de cette suite seront enregistres au fur et a mesure clans un fichier texte suite.txt a raison d'un terme par ligne.
Solution Algorithmique
Dans cet algorithme, On va utiliser trois fonctions et une procédure :
- la fonction saisie()
- la fonction max_entier ()
- la fonction min_entier ()
- la procédure remplir_fichier_suite ()
Algorithme du programme Principal
|
1 2 3 4 5 |
Algorithme suite Debut u0 <- saisie() # Saisie d'un nombre n positif forme de 4 chiffres remplir_fichier_suite(u0) # Génération et sauvegarde de la suite dans un fichier Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| u0 | entier |
La fonction saisir
Cette fonction saisit et retourne un entier positif formé de 4 chiffres .
|
1 2 3 4 5 6 7 8 9 10 |
Fonction saisie(): entier Ecrire('donner n forme de 4 chiffres: ') lire (n) # Tant que n n'a pas exactement 4 chiffres, on redemande Tant que (n < 1000) ou (n > 9999) faire Ecrire('donner n forme de 4 chiffres: ') lire (n) Fin tant que retourner n fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La fonction max_entier
La fonction max_entier(n) prend un nombre entier de quatre chiffres et construit, à partir de ses chiffres, le plus grand entier possible.
Pour cela, elle :
1- extrait les 4 chiffres du nombre n.
2- trie ces chiffres en ordre décroissant (du plus grand au plus petit) à l’aide d’un tri par sélection.
3- recompose un nouveau nombre à partir de ces chiffres triés.
4- retourne ce nombre, qui est donc le plus grand entier formé avec les chiffres de n.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
Fonction max_entier(n:entier):entier # Extraction des 4 chiffres du nombre t[0] <- n div 1000 # millier t[1] <- (n div 100) mod 10 # centaine t[2] <- (n div 10) mod 10 # dizaine t[3] <- n mod 10 # unité # Tri décroissant (sélection) des chiffres Pour i de 0 à 2 faire max_indice <- i Pour j de i+1 à 3 faire Si t[max_indice] < t[j] alors # Trouver le plus grand chiffre max_indice = j Fin si Fin pour # Échanger si un chiffre plus grand est trouvé Si max_indice != i alors temp <- t[i] t[i] <- t[max_indice] t[max_indice] <- temp Fin si Fin pour # Reconstruction du plus grand nombre max_n <- t[0]*1000 + t[1]*100 + t[2]*10 + t[3] retourner max_n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| j | entier |
| t | tableau des entiers |
| max_indice | entier |
| max_n | entier |
| temp | entier |
La fonction min_entier
La fonction min_entier(n) prend un nombre entier de quatre chiffres et construit, à partir de ses chiffres, le plus petit entier possible.
Pour cela, elle :
1- extrait les 4 chiffres du nombre n.
2- trie ces chiffres en ordre croissant (du plus petit au plus grand) à l’aide d’un tri par sélection.
3- recompose un nouveau nombre à partir de ces chiffres triés.
4- retourne ce nombre, qui est donc le plus petit entier formé avec les chiffres de n.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
Fonction min_entier(n:entier):entier # Extraction des 4 chiffres du nombre t[0] <- n div 1000 # millier t[1] <- (n div 100) mod 10 # centaine t[2] <- (n div 10) mod 10 # dizaine t[3] <- n mod 10 # unité # Tri croissant (sélection) des chiffres Pour i de 0 à 2 faire min_indice <- i Pour j de i+1 à 3 faire Si t[min_indice] > t[j] alors # Trouver le plus petit chiffre min_indice = j Fin si Fin pour # Échanger si un chiffre plus petit est trouvé Si min_indice != i alors temp <- t[i] t[i] <- t[min_indice] t[min_indice] <- temp Fin si Fin pour # Reconstruction du plus grand nombre min_n <- t[0]*1000 + t[1]*100 + t[2]*10 + t[3] retourner min_n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| j | entier |
| t | tableau des entiers |
| min_indice | entier |
| min_n | entier |
| temp | entier |
La procédure remplir_fichier_suite
La procédure remplir_fichier_suite(u0) sert à générer la suite définie par :𝑈𝑛+1=max_entier(𝑈𝑛) − min_entier(𝑈𝑛) et à enregistrer tous les termes de cette suite dans un fichier texte.
Plus précisément, cette procédure :
1- ouvre le fichier suite.txt en écriture.
2- écrit le premier terme U₀ dans le fichier.
3- calcule le terme suivant U₁ à l’aide de :
max_entier(u0) : plus grand nombre formé avec les chiffres de U₀
min_entier(u0) : plus petit nombre formé avec les mêmes chiffres
4- continue à calculer et écrire les termes suivants de la suite tant qu’ils sont différents du terme précédent (c’est-à-dire tant que la suite n’est pas stationnaire).
5- s’arrête automatiquement dès que la suite devient constante (Uₙ₊₁ = Uₙ).
6- Ferme le fichier une fois la suite terminée.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
Procédure remplir_fichier__suite(u0:entier): Ouvrir("suite.txt", f , "w") # Ouverture du fichier en écriture Ecrire(f,(Convch(u0) + '\n')) # Écrire le premier terme u0 dans le fichier u1 <- max_entier(u0) - min_entier(u0) # Calcul du terme suivant # Tant que la suite n’est pas stable, on continue Tant que u1 != u0 faire u0 <- u1 Ecrire(f,(Convch(u0) + '\n')) # Écrire le nouveau terme u0 dans le fichier u1 <- max_entier(u0) - min_entier(u0) # Calcul du terme suivant pour i de 0 à n faire Fin tant que fermer(f) fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| f | fichier du nombre.dat |
| u1 | entier |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 |
from numpy import * t = array([int()] * 10) # Tableau utilisé pour stocker temporairement les chiffres du nombre # ------------------------------- # Procédure de saisie d’un nombre # ------------------------------- def saisie(): n = int(input('donner n forme de 4 chiffres: ')) # Tant que n n'a pas exactement 4 chiffres, on redemande while (n < 1000) or (n > 9999): n = int(input('donner n forme de 4 chiffres: ')) return n # --------------------------------------------------------- # Fonction qui construit le plus grand entier formé # en réarrangeant les 4 chiffres du nombre donné # --------------------------------------------------------- def max_entier(n): # Extraction des 4 chiffres du nombre t[0] = n // 1000 # millier t[1] = (n // 100) % 10 # centaine t[2] = (n // 10) % 10 # dizaine t[3] = n % 10 # unité # Tri décroissant (sélection) des chiffres for i in range(3): max_indice = i for j in range(i+1, 4): if t[max_indice] < t[j]: # Trouver le plus grand chiffre max_indice = j # Échanger si un chiffre plus grand est trouvé if max_indice != i: temp = t[i] t[i] = t[max_indice] t[max_indice] = temp # Reconstruction du plus grand nombre max_n = t[0]*1000 + t[1]*100 + t[2]*10 + t[3] return max_n # --------------------------------------------------------- # Fonction qui construit le plus petit entier formé # en réarrangeant les 4 chiffres du nombre donné # --------------------------------------------------------- def min_entier(n): # Extraction des 4 chiffres t[0] = n // 1000 t[1] = (n // 100) % 10 t[2] = (n // 10) % 10 t[3] = n % 10 # Tri croissant (sélection) des chiffres for i in range(3): min_indice = i for j in range(i, 4): if t[min_indice] > t[j]: # Trouver le plus petit chiffre min_indice = j # Échange si nécessaire if min_indice != i: temp = t[i] t[i] = t[min_indice] t[min_indice] = temp # Reconstruction du plus petit nombre min_n = t[0]*1000 + t[1]*100 + t[2]*10 + t[3] return min_n # --------------------------------------------------------- # Fonction qui génère la suite u(n+1) = max(u_n) - min(u_n) # et l’enregistre dans un fichier jusqu’à stabilisation # --------------------------------------------------------- def remplir_fichier_suite(u0): f = open("suite.txt", "w") # Ouverture du fichier en écriture f.write(str(u0) + '\n') # Écrire le premier terme u1 = max_entier(u0) - min_entier(u0) # Calcul du terme suivant # Tant que la suite n’est pas stable, on continue while u1 != u0: u0 = u1 f.write(str(u0) + '\n') # Enregistrer le terme dans le fichier u1 = max_entier(u0) - min_entier(u0) f.close() # Fermeture du fichier # --------------------- # Programme principal # --------------------- u0 = saisie() # Saisie du nombre de départ remplir_fichier_suite(u0) # Génération et sauvegarde de la suite |
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés