Super premier – Bac pratique – Section informatique- 2009

Sujet (Algo et programmation - Bac 2009)
Un nombre est dit super premier s'il est premier et si, en supprimant des chiffres à partir de sa droite, le nombre restant est aussi premier.
Exemple : Le nombre 59399 est super premier car les nombres 59399, 5939, 593, 59 et 5 sont tous premiers.
Ecrire un programme en Python qui permet de :
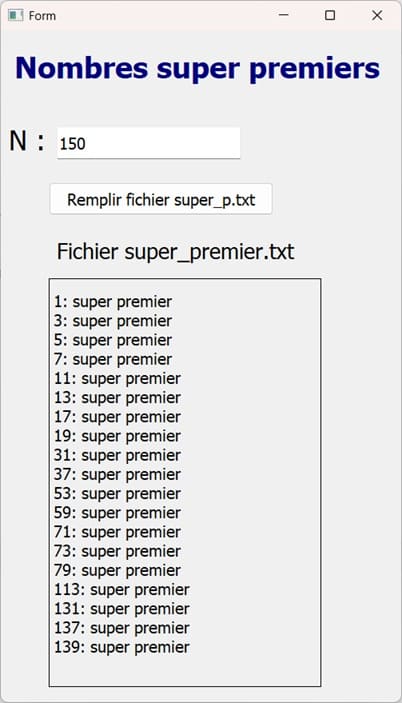
- saisir un entier n tel que 40000 < n < 100000, - chercher tous les nombres premiers inférieurs ou égaux à n, les afficher à raison d'un nombre par ligne en mentionnant devant chaque nombre super premier la note « super premier » et de faire la même chose dans un fichier texte intitulé super_p.txt.
Solution Algorithmique
Dans cet algorithme, On va utiliser trois fonctions et une procédure :
- la fonction saisie()
- la fonction test_premier()
- la fonction test_superpremier()
- la procédure remplir_fichier_superpremier ()
Algorithme du programme Principal
|
1 2 3 4 5 |
Algorithme super_premiers Debut n <- saisie() # Saisie d'un nombre n (40000 < n < 100000) remplir_fichier_superpremier(n) # Remplir le fichier avec les super premiers jusqu'à Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La fonction saisir
Cette fonction saisit et retourne un entier entre 40000 et 10000.
|
1 2 3 4 5 6 7 8 9 10 |
Fonction saisie(): entier Ecrire('donner n telque 10<n<100: ') lire (n) # Tant que n n'est pas dans l'intervalle demandé, on redemande Tant que (n <= 40000) ou (n >= 100000) faire Ecrire('donner n telque 40000<n<100000: ') lire (n) Fin tant que retourner n fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La fonction test_premier
La fonction test_premier(n) a pour rôle de déterminer si un nombre entier n est un nombre premier.
Comment elle fonctionne ?
1- Elle commence par tester les diviseurs possibles à partir de 2.
2- Elle cherche un entier i qui divise n (autre que 1 et n).
3- Tant qu’aucun diviseur n’est trouvé et que i est inférieur ou égal à la moitié de n, elle continue d’incrémenter i.
4- À la fin :
Si aucun diviseur n’a été trouvé, la fonction retourne Vrai → le nombre est premier.
Si un diviseur a été trouvé, la fonction retourne Faux → le nombre n’est pas premier.
|
1 2 3 4 5 6 7 8 9 |
fonction test_premier(n:entier):booleen i <- 2 # On cherche un diviseur i tant que i ne divise pas n et que i <= n div 2 Tant que (n mod i != 0 and i <= n div 2) faire i <- i + 1 Fin tant que # Si aucun diviseur trouvé, alors n est premier retourner n mod i != 0 Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
La fonction test_superpremier
Cette fonction compte combien de fois le caractère c (par exemple '0' ou '1') apparaît dans la chaîne binaire.
Plus précisément :
1- Elle parcourt toute la chaîne binaire caractère par caractère.
2- Chaque fois qu’elle trouve le caractère recherché c, elle incrémente un compteur.
3- À la fin, elle retourne le nombre total d'occurrences du caractère.
|
1 2 3 4 5 6 7 8 |
Fonction test_superpremier(n:entier) : booleen # Tant que n est premier et a au moins deux chiffres Tant que test_premier(n) et (n >= 10) faire n = n // 10 # On enlève le dernier chiffre de n Fin tant que # Pour être super premier, le dernier sous-nombre doit être premier également retourner test_premier(n) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| cp | entier |
| i | entier |
La procédure remplir_fichier_superpremier
La procédure remplir_fichier_superpremier(n) parcourt tous les nombres entre 0 et n, teste si chacun d’eux est super premier grâce à la fonction test_superpremier(i), et enregistre dans un fichier texte ceux qui vérifient cette propriété.
Plus précisément, elle :
1- ouvre un fichier texte super_p.txt en écriture pour y stocker les nombres super premiers trouvés.
2- parcourt tous les entiers de 0 jusqu’à n
3- teste si chaque entier i est super premier grâce à la fonction test_superpremier(i) (déjà définie ailleurs).
4- Si le nombre est super premier :
Elle l’affiche sur l’écran
Elle l’écrit dans le fichier sous la forme : i : super premier
5- ferme le fichier une fois l’écriture terminée.
|
1 2 3 4 5 6 7 8 9 |
Procédure remplir_fichier_superpremier(n:entier): Ouvrir("super_p.txt", f , "w") # Ouverture du fichier en écriture pour i de 0 à n faire Si test_superpremier(i) alors # Si i est super premier Ecrire((Convch(i) + ': super premier \n')) Ecrire(f,(convch(i) + ': super premier \n')) # On écrit dans le fichier fin pour fermer(f) fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| f | fichier du nombre.dat |
| i | entier |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 |
# Fonction pour saisir un nombre n compris entre 40 000 et 100 000 def saisie(): n = int(input('donner n telque 40000<n<100000: ')) # Tant que n n'est pas dans l'intervalle demandé, on redemande sa saisie while (n <= 40000) or (n >= 100000): n = int(input('donner n telque 40000<n<100000: ')) return n # Fonction pour tester si un nombre est premier def test_premier(n): i = 2 # On cherche un diviseur i tant que i ne divise pas n et que i <= n//2 while (n % i != 0 and i <= n // 2): i = i + 1 # Si aucun diviseur trouvé, alors n est premier return n % i != 0 # Fonction pour tester si un nombre est "super premier" # Un nombre est super premier si : # - il est premier # - en supprimant son dernier chiffre successivement, tous les sous-nombres sont premiers def test_superpremier(n): # Tant que n est premier et a au moins deux chiffres while test_premier(n) and (n >= 10): n = n // 10 # On enlève le dernier chiffre de n # Pour être super premier, le dernier sous-nombre doit être premier également return test_premier(n) # Fonction pour remplir un fichier avec les nombres super premiers de 0 à n def remplir_fichier_superpremier(n): f = open("super_p.txt", "w") # Ouverture du fichier en écriture # On teste tous les nombres entre 0 et n for i in range(n + 1): if test_superpremier(i): # Si i est super premier print((str(i) + ': super premier \n')) f.write(str(i) + ': super premier \n') # On écrit dans le fichier f.close() # Fermeture du fichier # Programme principal n = saisie() # Saisie du nombre n remplir_fichier_superpremier(n) # Remplir le fichier avec les super premiers jusqu'à n |
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés