Calcul du PPCM – Bac pratique – Section informatique – 2019

Sujet (Algo et programmation - Bac 2019)
Parmi les méthodes utilisées pour calculer le Plus Petit Commun Multiple (PPCM) de deux entiers a et b, on cite la suivante :
- On procède à la décomposition de chaque entier en produit de facteurs premiers sous forme de
- Le PPCM est égal au produit de tous les facteurs premiers, communs ou non, chacun est élevé à son exposant le plus grand.
NB :
1- La décomposition d'un entier k en un produit de facteurs premiers consiste à écrire cet entier sous forme d'un produit de nombres premiers. Pour ce faire, on peut procéder comme suit :
2- Vérifier si k est divisible par 2 (le plus petit nombre premier).
Si oui, diviser k par 2 et le remplacer par k div 2 (le quotient de la division) jusqu'à obtenir un reste différent de O.
a- Refaire l'étape précédente pour les nombres premiers suivants (3, 5, 7, ...) jusqu'à obtenir un quotient égal à 1.
b- Un nombre premier est un entier naturel, strictement supérieur à 1, divisible uniquement par 1 et par lui-même.
Exemple 1 :
Pour a = 168 et b = 36, le calcul du PPCM se présente comme suit :
Décomposition de chaque entier en produit de facteurs premiers, sous forme de puissances
168=2 * 2 * 2 * 3 * 7 = 23 * 31 * 71
36=2 * 2 * 2 * 3 * 3 = 22 * 32
Le PPCM (168,36) = 23 * 32 * 71 = 5.4
Exemple 2 :
Pour a = 24 et b = 35, le calcul du PPCM se présente comme suit :
Décomposition de chaque entier en produit de facteurs premiers, sous forme de puissances :
24=2*2*2*3=23*31
35 = 5 * 7 = 51 * 71
Le PPCM (24, 35) = 23 * 31 * 51 * 71 = 840
On se propose de créer et de remplir un fichier d'enregistrements intitulé "F_PPCM.dat" dont chaque enregistrement contient les trois champs a, b et PPCM tel que la valeur du champ PPCM est égale au Plus Petit Commun Multiple des deux entiers a et b calculé en utilisant la méthode expliquée ci-dessus.
Travail demandé :
Ecrire un programme en Python intitulé "CalcPPCM" qui permet :
- de saisir un entier N représentant le nombre d'enregistrements du fichier "F_PPCM.dat" (avec 2 <= N <= 100), - de créer et de remplir le fichier d'enregistrements "F_PPCM.dat" tel que :
a et b sont des entiers strictement positifs inférieurs à 1000 et dont les valeurs sont lues à partir du clavier.
PPCM est calculé comme décrit précédemment.
- d'afficher le contenu du fichier "F PPCM.dat" en respectant la forme suivante : PPCM(a, b) = PPCM
Solution Algorithmique
Dans cet algorithme, On va utiliser deux fonctions et trois procédures:
- la fonction saisie()
- la procédure factoriel_premiers()
- la fonction calcul_ppcm()
- la procédure remplir_fichier()
- la procédure afficher_fichier()
Algorithme du programme Principal
|
1 2 3 4 5 6 |
Algorithme CalcPPCM Debut n <- saisie(2, 100) # Nombre de calculs PPCM remplir_fichier(n) # Remplissage du fichier afficher_fichier() # Affichage du contenu Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La fonction saisie
Cette fonction permet de saisir un entier valide compris entre deux bornes inf et sup.
1- Elle demande à l’utilisateur de saisir un entier n.
2- Elle vérifie que n appartient à l’intervalle [𝑖𝑛𝑓,𝑠𝑢𝑝]
3- Si la valeur saisie n’est pas valide, la fonction redemande la saisie jusqu’à obtenir un entier correct.
4- Elle retourne finalement la valeur valide saisie par l’utilisateur.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
Fonction saisie():entier # Saisie initiale Ecrire('donner n tel que ' ,inf , '<= n <= ' , sup, ': ') Lire(n) # Répéter la saisie tant que n n'est pas valide Tant que Non(inf <= n <= sup) faire Ecrire('donner n tel que ' ,inf , '<= n <= ' , sup, ': ') Lire(n) Fin tant que # Retourner la valeur correcte retourner n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La procédure factoriel_premiers
Cette procédure permet de décomposer un nombre entier n en facteurs premiers et de stocker ces facteurs dans le tableau t.
1- Le tableau t est d’abord initialisé à 0 pour effacer les anciennes valeurs.
2- On commence la recherche des diviseurs à partir de 2, le plus petit nombre premier.
3- Tant que n est différent de 1 :
Si i divise n, alors : i est un facteur premier de n. Alors on divise n par i et on stocke i dans le tableau t
Sinon, on passe au diviseur suivant.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
Procedure factoriel_premiers(n:entier, t:tableau): index <- 0 # Indice du tableau t # Initialisation du tableau t à 0 Pour k de 0 à 49 faire t[k] <- 0 Fin pour i <- 2 # Premier diviseur possible # Décomposition en facteurs premiers Tant que n != 1 faire Si n mod i = 0 alors n <- n div i t[index] <- i index <- index + 1 Sinon i <- i + 1 Fin si Fin tant que Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| index | entier |
| k | entier |
| i | entier |
La fonction calcul_ppcm
Cette fonction permet de calculer le Plus Petit Commun Multiple (PPCM) de deux nombres à partir de leurs facteurs premiers stockés dans les tableaux t1 et t2.
Principe de fonctionnement
1- Initialisation
i = 0 : sert à parcourir les deux tableaux.
ppcm = 1 : variable qui contiendra le PPCM final.
2- Parcours simultané des deux tableaux
Tant qu’on a des facteurs dans les deux tableaux (t1[i] != 0 et t2[i] != 0) :
Si les facteurs sont identiques, on multiplie le PPCM par ce facteur. Sinon, on multiplie le PPCM par les deux facteurs différents.
L’indice i est incrémenté pour passer au facteur suivant.
3- Ajout des facteurs restants
Si un tableau a encore des facteurs après la fin du parcours commun, on les multiplie au PPCM :
Tant que t1[i] != 0 → multiplie le PPCM par les facteurs restants de t1.
Tant que t2[i] != 0 → multiplie le PPCM par les facteurs restants de t2.
4- Retour du résultat
La fonction retourne la valeur finale du PPCM.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
Fonction calcul_ppcm(t1:tableau;t2:tableau i <- 0 ppcm <- 1 # Parcours simultané des deux tableaux Tant que t1[i] != 0 et t2[i] != 0 faire Si t1[i] = t2[i] alors ppcm <- ppcm * t1[i] Sinon a <- t1[i] b <- t2[i] ppcm <- ppcm * a * b Fin si i <- i + 1 Fin tant que # Ajout des facteurs restants de t1 Tant que t1[i] != 0 faire ppcm <- ppcm * t1[i] i <- i + 1 Fin tant que # Ajout des facteurs restants de t2 Tant que t2[i] != 0 faire ppcm <- ppcm * t2[i] i <- i + 1 Fin tant que retourner ppcm Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| ppcm | entier |
La procédure remplir_fichier
Cette procédure sert à remplir un fichier nommé F_PPCM.dat avec le PPCM de plusieurs couples de nombres saisis par l’utilisateur.
1- Affichage d’un message d’information
Il indique à l’utilisateur que le fichier va être rempli.
2- Ouverture du fichier
Le fichier est ouvert en mode écriture ("w").
Si le fichier existe déjà, son contenu est effacé.
3- Saisie des couples de nombres :
La procédure demande à l’utilisateur de saisir n couples de nombres.
La fonction saisie garantit que les nombres sont compris entre 1 et 1000.
4- Décomposition en facteurs premiers
Chaque nombre est décomposé en facteurs premiers.
Les facteurs sont stockés dans les tableaux t1 et t2.
5- Calcul du PPCM
La procédure utilise la fonction calcul_ppcm pour obtenir le PPCM du couple.
6- Écriture dans le fichier
Chaque résultat est écrit dans le fichier sous la forme : PPCM(a, b) = résultat
7- Fermeture du fichier
La procédure libère le fichier et sauvegarde toutes les données.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
Procedure remplir_fichier(n:entier) Ecrire('*** Remplir fichier F_PPCM.dat ***') # Ouverture du fichier en mode écriture Ouvri(f , "F_PPCM.dat", "w") # Saisie de n couples de nombres Pour i de 0 à n-1 faire a <- saisie(1, 1000) b <- saisie(1, 1000) # Décomposition en facteurs premiers factoriel_premiers(a, t1) factoriel_premiers(b, t2) # Calcul du PPCM ppcm <- calcul_ppcm(t1, t2) # Écriture du résultat dans le fichier Ecrire(f , 'PPCM(' + Convch(a) + ',' + Convch(b) + ') = ' + Convch(ppcm) + '\n') Fin pour # Fermeture du fichier Fermer(f) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| a | entier |
| b | entier |
| ppcm | entier |
| t1 | tableau |
| t2 | tableau |
| f | fichier |
La procédure afficher_fichier
Cette procédure sert à lire et afficher le contenu du fichier F_PPCM.dat créé précédemment, pour que l’utilisateur puisse voir les résultats des calculs de PPCM.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
Procédure afficher_fichier() Ecrire('*** Contenu fichier F_PPCM.dat ***') # Ouverture du fichier en mode lecture Ouvri(f , "F_PPCM.dat", "r") lignes <- Lire_lignes(f) # Affichage de chaque ligne Pour ligne dans lignes faire Ecrire(ligne) Fin pour # Fermeture du fichier Fermer(f) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| f | fichier |
| lignes | chaîne |
| ligne | chaîne |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 |
from numpy import * # -------------------------------------------------- # Déclaration de deux tableaux de taille 50 # Ils serviront à stocker les facteurs premiers # -------------------------------------------------- t1 = array([int()] * 50) t2 = array([int()] * 50) # -------------------------------------------------- # Fonction de saisie sécurisée # Elle force l'utilisateur à saisir un entier # compris entre inf et sup # -------------------------------------------------- def saisie(inf, sup): # Saisie initiale n = int(input('donner un nombre entre ' + str(inf) + ' et ' + str(sup) + ' : ')) # Vérification de la validité de la saisie while not (inf <= n <= sup): n = int(input('donner un nombre entre ' + str(inf) + ' et ' + str(sup) + ' : ')) # Retour de la valeur valide return n # -------------------------------------------------- # Procédure qui décompose un nombre n # en facteurs premiers # Les facteurs sont stockés dans le tableau t # -------------------------------------------------- def factoriel_premiers(n, t): index = 0 # Indice du tableau t # Initialisation du tableau t à 0 for k in range(50): t[k] = 0 i = 2 # Premier diviseur possible # Décomposition en facteurs premiers while n != 1: if n % i == 0: n = n // i t[index] = i index = index + 1 else: i = i + 1 # -------------------------------------------------- # Fonction qui calcule le PPCM de deux nombres # à partir de leurs facteurs premiers stockés # dans t1 et t2 # -------------------------------------------------- def calcul_ppcm(t1, t2): i = 0 ppcm = 1 # Parcours simultané des deux tableaux while t1[i] != 0 and t2[i] != 0: if t1[i] == t2[i]: ppcm = ppcm * t1[i] else: a = t1[i] b = t2[i] ppcm = ppcm * a * b i = i + 1 # Ajout des facteurs restants de t1 while t1[i] != 0: ppcm = ppcm * t1[i] i = i + 1 # Ajout des facteurs restants de t2 while t2[i] != 0: ppcm = ppcm * t2[i] i = i + 1 return ppcm # -------------------------------------------------- # Procédure qui remplit le fichier F_PPCM.dat # avec les PPCM de couples de nombres saisis # -------------------------------------------------- def remplir_fichier(n): print('*** Remplir fichier F_PPCM.dat ***') # Ouverture du fichier en mode écriture f = open("F_PPCM.dat", "w") # Saisie de n couples de nombres for i in range(n): a = saisie(1, 1000) b = saisie(1, 1000) # Décomposition en facteurs premiers factoriel_premiers(a, t1) factoriel_premiers(b, t2) # Calcul du PPCM ppcm = calcul_ppcm(t1, t2) # Écriture du résultat dans le fichier f.write('PPCM(' + str(a) + ',' + str(b) + ') = ' + str(ppcm) + '\n') # Fermeture du fichier f.close() # -------------------------------------------------- # Procédure qui affiche le contenu du fichier # F_PPCM.dat # -------------------------------------------------- def afficher_fichier(): print('*** Contenu fichier F_PPCM.dat ***') # Ouverture du fichier en mode lecture f = open("F_PPCM.dat", "r") lignes = f.readlines() # Affichage de chaque ligne for ligne in lignes: print(ligne.strip('\n')) # Fermeture du fichiera f.close() # -------------------------------------------------- # Programme principal # -------------------------------------------------- n = saisie(2, 100) # Nombre de calculs PPCM remplir_fichier(n) # Remplissage du fichier afficher_fichier() # Affichage du contenu |
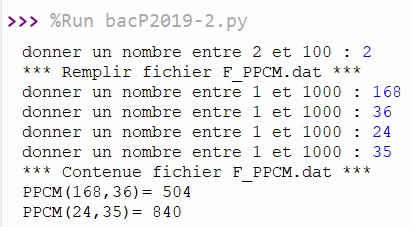
Exécution du programme
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés