Diviseurs unitaires – Bac informatique pratique scientifique 2025

Algo et Python 30-09-25

43 0

Sujet bac informatique pratique (Bac scientifique 2025)

On se propose de concevoir une interface graphique permettant de saisir un entier naturel N composé de trois chiffres et d’afficher ses diviseurs unitaires s’ils existent.

On dit qu’un entier A est un diviseur unitaire d’un entier N si et seulement s’il existe un entier B tels que :

N = A * B

A est composé d’un seul chiffre différent de 1.

A et B sont premiers entre eux. Deux entiers sont dits premiers entre eux si leur plus grand commun diviseur (PGCD) est égal à 1.

Exemples :

1) Pour N = 252

252 = 4 * 63

4 est composé d’un seul chiffre

4 et 63 sont premiers entre eux car PGCD (4,63) = 1

252 = 7 * 36

7 est composé d’un seul chiffre

7 et 36 sont premiers entre eux car PGCD (7,36) = 1

252 = 9 * 28

9 est composé d’un seul chiffre

9 et 28 sont premiers entre eux car PGCD (9,28) = 1

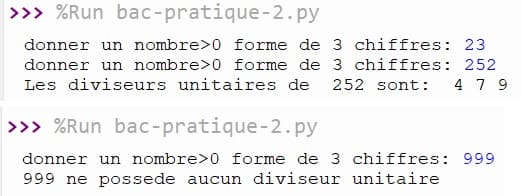
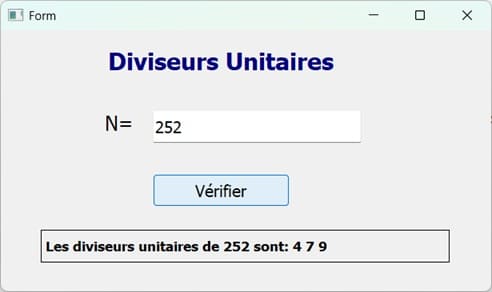
Le programme affiche : Les diviseurs unitaires de 252 sont : 4, 7, 9

2) Pour N = 901

N n’a aucun diviseur formé d’un seul chiffre.

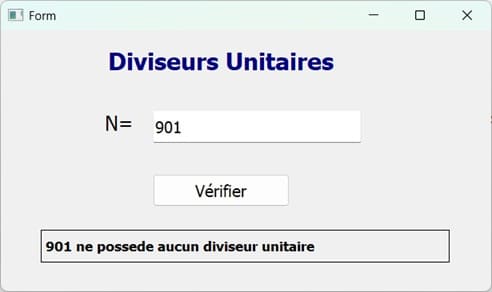
Le programme affiche : 901 ne possède aucun diviseur unitaire

3) Pour N = 999

999 = 3 * 333

3 est composé d’un seul chiffre

3 et 333 ne sont pas premiers entre eux car PGCD (3,333) = 3 ≠ 1

999 = 9 * 111

9 est composé d’un seul chiffre

9 et 111 ne sont pas premiers entre eux car PGCD (9,111) = 3 ≠ 1

Le programme affiche : 999 ne possède aucun diviseur unitaire

Solution Algorithmique

L’algorithme a pour rôle de :

1- lire un entier naturel N composé de trois chiffres (entre 100 et 999).

2- rechercher les diviseurs unitaires de N, c’est-à-dire les entiers A qui : sont constitués d’un seul chiffre compris entre 2 et 9, divisent N (N = A × B), et sont premiers avec B (c’est-à-dire que PGCD(A, B) = 1).

3- afficher les diviseurs unitaires trouvés si au moins un existe.

Sinon, afficher un message signalant que le nombre N ne possède aucun diviseur unitaire.

Dans cet algorithme, On va utiliser trois fonctions :

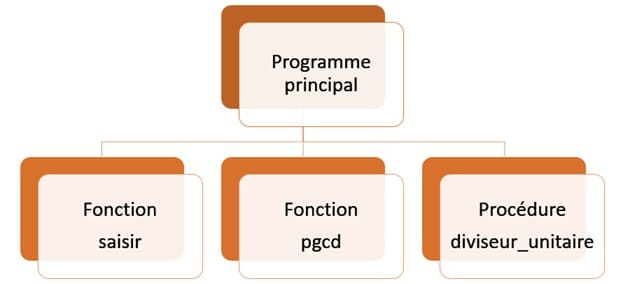
Algorithme du programme Principal

Algorithme diviseurs_unitaires
Debut
     n<-saisie()
     diviseur_unitaire(n)
Fin

Algorithme diviseurs_unitaires

Debut

n<-saisie()

diviseur_unitaire(n)

Fin

Déclaration des objets

Objet	Type / Nature
n	entier

La fonction saisir

Cette fonction saisit un nombre entier N strictement positif qui contient au moins trois chiffres

fonction saisie():entier
Début
       Ecrire("donner un nombre>0 forme de 3 chiffres:")
       Lire(n)
       Tant que (n<100) ou (n>999) aire
           Ecrire("donner un nombre>0 forme de 3 chiffres:") 
           Lire(n)
       Fin tant que
       retourner n
Fin

fonction saisie():entier

Début

Ecrire("donner un nombre>0 forme de 3 chiffres:")

Lire(n)

Tant que (n<100) ou (n>999) aire

Ecrire("donner un nombre>0 forme de 3 chiffres:")

Lire(n)

Fin tant que

retourner n

Fin

Déclaration des objets

Objet	Type / Nature
n	entier

La fonction pgcd

Cette fonction permet de déterminer le plus grand commun diviseur de deux entiers a et a.

fonction pgcd(a,b:entier): entier 
Début
      Tant que (b!=0) faire
         r<-a div b
         a<-b
         b<-r
      
     retourner a 
Fin

fonction pgcd(a,b:entier): entier

Début

Tant que (b!=0) faire

r<-a div b

a<-b

b<-r

retourner a

Fin

Déclaration des objets

Objet	Type / Nature
r	entier

La procédure diviseur_unitaire

Cette procédure recherche et affiche les diviseurs unitaires de N, c’est-à-dire les entiers A qui sont constitués d’un seul chiffre compris entre 2 et 9, divisent N (N = A × B), et sont premiers avec B (c’est-à-dire que PGCD(A, B) = 1).

Procédure diviseur_unitaire (n:entier)
Début
     liste_diviseurs_unitaires<-""
     pour i de 2 à 10 faire
        Si (n div i = 0) alors
          Si (pgcd(i,n/i)=1) alors
              liste_diviseurs_unitaires<-liste_diviseurs_unitaires+i+" "
          Fin si
        Fin si 
     Fin pour
     Si long(liste_diviseurs_unitaires)!=0 alors
        Ecrire('Les diviseurs unitaires de ',n,'sont: ',liste_diviseurs_unitaires)
     Sinon 
        Ecrire(n,'ne possede aucun diviseur unitaire')
     Finsi
Fin

Procédure diviseur_unitaire (n:entier)

Début

liste_diviseurs_unitaires<-""

pour i de 2 à 10 faire

Si (n div i = 0) alors

Si (pgcd(i,n/i)=1) alors

liste_diviseurs_unitaires<-liste_diviseurs_unitaires+i+" "

Fin si

Fin pour

Si long(liste_diviseurs_unitaires)!=0 alors

Ecrire('Les diviseurs unitaires de ',n,'sont: ',liste_diviseurs_unitaires)

Sinon

Ecrire(n,'ne possede aucun diviseur unitaire')

Finsi

Fin

Déclaration des objets

Objet	Type / Nature
i	entier
liste_diviseurs_unitaires	chaine

Solution en Python

def saisir():
    n=int(input("donner un nombre>0 forme de 3 chiffres: "))
    while (n<100) or (n>999) :
       n=int(input("donner un nombre>0 forme de 3 chiffres: "))
    return n

def pgcd(a,b):
    while (b!=0) :
        r=a % b
        a=b
        b=r
    return a   

def diviseur_unitaire(n):
    liste_diviseurs_unitaires=""
    for i in range(2,10):
        if (n % i == 0):
           if (pgcd(i,n/i)==1):
               liste_diviseurs_unitaires=liste_diviseurs_unitaires+str(i)+" "
    if len(liste_diviseurs_unitaires)!=0 :
        print('Les diviseurs unitaires de ',n,'sont: ',liste_diviseurs_unitaires)
    else:
        print(n,'ne possede aucun diviseur unitaire')
      

#programme principal

n=saisir()
diviseur_unitaire(n)

def saisir():

n=int(input("donner un nombre>0 forme de 3 chiffres: "))

while (n<100) or (n>999) :

n=int(input("donner un nombre>0 forme de 3 chiffres: "))

return n

def pgcd(a,b):

while (b!=0) :

r=a % b

a=b

b=r

return a

def diviseur_unitaire(n):

liste_diviseurs_unitaires=""

for i in range(2,10):

if (n % i == 0):

if (pgcd(i,n/i)==1):

liste_diviseurs_unitaires=liste_diviseurs_unitaires+str(i)+" "

if len(liste_diviseurs_unitaires)!=0 :

print('Les diviseurs unitaires de ',n,'sont: ',liste_diviseurs_unitaires)

else:

print(n,'ne possede aucun diviseur unitaire')

#programme principal

n=saisir()

diviseur_unitaire(n)

Exécution du programme :

Solution en Python et Designer QT

Pour créer une application en Python et Designer QT afin de saisir un entier naturel N composé de trois chiffres et d’afficher ses diviseurs unitaires s’ils existent, on va suivre ces étapes:

1- Créer l'interface graphique avec Qt Designer

a- Ouvrez Qt Designer et créez un nouveau fichier de type Main Window.

b- Ajoutez ces widgets:

QLabel nommé 'msg' pour afficher les messages générés par le programme

QLineEdit nommé 'n' pour entrer le nombre N

QPushButton nommé 'vrifier_bt' pour chercher et afficher les diviseurs unitaires du nombre N

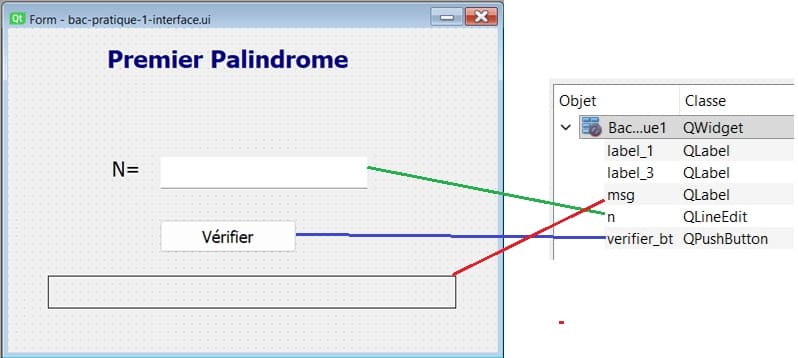
Enregistrez le fichier avec l'extension .ui, par exemple bac-pratique-2-interface.ui.ui.

2- Créer le script Python pour l'application

Voici un exemple de script Python qui utilise l'interface graphique générée par Qt Designer.

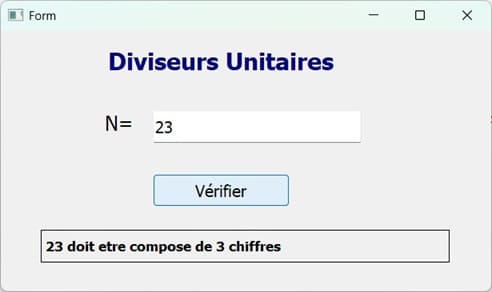
from PyQt5.uic import loadUi
from PyQt5.QtWidgets import QApplication


app = QApplication([])
windows = loadUi ("bac-pratique-2-interface.ui")

def pgcd(a,b):
    while (b!=0) :
        r=a % b
        a=b
        b=r
    return a   

   
def play():
 windows.msg.clear() 
 n = int(windows.n.text())
 
 if  (n>=100) and (n<=999): 
   liste_diviseurs_unitaires=""
   for i in range(2,10):
        if (n % i == 0):
           if (pgcd(i,n/i)==1):
               liste_diviseurs_unitaires=liste_diviseurs_unitaires+str(i)+" "
   if len(liste_diviseurs_unitaires)!=0 :
        windows.msg.setText('Les diviseurs unitaires de '+str(n)+' sont: '+liste_diviseurs_unitaires)
   else:
        windows.msg.setText(str(n)+' ne possede aucun diviseur unitaire')     
 else:
      windows.msg.setText(str(n)+' doit etre compose de 3 chiffres') 
         
   
windows.verifier_bt.clicked.connect(play)

windows.show()
app.exec_()