Divisibilité par 13 et 7 – Bac pratique – Section informatique – 2020

Sujet (Algo et programmation - Bac 2020)
Soit "Nombre.txt" un fichier texte contenant des entiers naturels à raison d’un entier par ligne. On se propose de créer deux fichiers textes "Div13.txt" et "Div7.txt" contenant respectivement les valeurs, de "Nombre.txt", qui sont divisibles par 13 et par 7 à raison d’un entier par ligne en se basant sur les deux principes décrits ci-après :
A- Divisibilité par 13
L’algorithme du module Divis13 ci-après permet de vérifier si un nombre N est divisible par 13.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
Fonction Divis13(N:chaine):booléen Début s<-0 sg<--1 Tant que long(n)>3 faire v <- Valeur(Sous_chaine(n, long(n)-3, long(n))) s <- s+v*sg sg <- -sg n <- Sous_chaine(n, 0 , long(n)-3) Fin tant que v <- Valeur(n) s <- s+v*sg retourner abs(s) div 1 ==0 Fin |
Exemple :
Pour vérifier si le nombre 1612311857 est divisible par 13, on applique la règle de divisibilité par 13 décrite par l’algorithme précédent :
- On regroupe les chiffres du nombre par des blocs de trois chiffres en commençant à partir des unités : 1 | 612 | 311 | 857
- On ajoute alternativement des "–" et des "+" entre les blocs en commençant par placer un "–" pour le premier bloc à droite : 1 – 612 + 311 – 857
- On effectue l’opération ainsi obtenue : 1 – 612 + 311 – 857 = –1157
- La valeur absolue du résultat obtenu (1157) est divisible par 13 donc 1612311857 est divisible par 13. B- Divisibilité par 7
Pour vérifier si un nombre N est divisible par 7 nous proposons la règle de divisibilité suivante :
- Calculer la somme itérée et pondérée des chiffres de N par la série périodique de période 1, 3, 2, −1, −3, −2, c’est-à-dire additionner tous les chiffres de N en multipliant chacun par un chiffre de la période en commençant par le chiffre des unités qui sera multiplié par 1, le chiffre des dizaines sera multiplié par 3, ... . Si la somme est un nombre formé de plus d’un chiffre, on recommence le processus.
Exemple : Pour N = 45286090 la somme itérée et pondérée est égale à 3. En effet :
0 x 1 + 9 x 3 + 0 x 2 + 6 x (−1) + 8 x (−3) + 2 x (−2) + 5 x 1 + 4 x 3 = 10
Comme 10 est composé de plus d’un chiffre alors on recommence le processus avec 10, d’où : 0 x 1 + 1 x 3 = 3
- Un nombre N est divisible par 7 si la somme itérée et pondérée de ses chiffres par la série périodique de période 1, 3, 2, −1, −3, −2 vaut 0 ou 7.
Exemples :
- 6090 est divisible par 7, en effet : 0 x 1 + 9 x 3 + 0 x 2 + 6 x (−1) = 21. Comme 21 est composé de plus d’un chiffre alors on recommence le processus d’où 1 x 1 + 2 x 3 = 7
- 717255 est divisible par 7, en effet : 5 x 1 + 5 x 3 + 2 x 2 + 7 x (−1) + 1 x (−3) + 7 x (−2) = 0
- 45286090 n’est pas divisible par 7, en effet : 0 x 1 + 9 x 3 + 0 x 2 + 6 x (−1) + 8 x (−3) + 2 x (−2) + 5 x 1 + 4 x 3 = 10
Comme 10 est composé de plus d’un chiffre alors on recommence le processus d’où 0 x 1 + 1 x 3 = 3 Comme 3 est différent de 0 et de 7 donc 45286090 n’est pas divisible par 7
Travail demandé :
Ecrire un programme en Python qui permet de :
- Saisir Nb entiers naturels (Nb≥ 5) à enregistrer dans le fichier "Nombre.txt"
- Placer les nombres du fichier "Nombre.txt" qui sont divisibles par 13 dans un fichier nommé "Div13.txt" en utilisant le module Divis13 et les nombres divisibles par 7 dans un fichier nommé "Div7.txt" en appliquant la règle de divisibilité par 7 expliquée ci-dessus.
Solution Algorithmique
Dans cet algorithme, On va utiliser trois fonctions et six procédures:
- la fonction saisie()
- la procédure remplir_fichier_nombre()
- la fonction divis13()
- la fonction divis7()
- la procédure remplir_fichiers_div()
- la procédure afficher_fichiers_div()
Algorithme du programme Principal
|
1 2 3 4 5 6 7 8 |
Algorithme divisibilite_13_7 Debut n <- saisie() # Saisie du nombre d'entiers remplir_fichier_nombre(n) # Remplissage du fichier Nombre.txt remplir_fichiers_div() # Remplissage des fichiers Div13.txt et Div7.txt afficher_fichiers_div("Div13.txt") # Affichage des nombres divisibles par 13 afficher_fichiers_div("Div7.txt") # Affichage des nombres divisibles par 7 Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La fonction saisie
Cette fonction a pour objectif de demander à l’utilisateur de saisir un entier supérieur ou égal à 5 et de s’assurer que la saisie est valide avant de la retourner.
Elle garantit qu’on obtient toujours un entier ≥ 5, évitant ainsi les erreurs liées à une saisie incorrecte.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
Fonction saisie():entier # Saisie initiale Ecrire('donner un nombre >=5: ') Lire(n) # Vérification de la validité de la saisie Tant que Non(n >= 5) faire Ecrire('donner un nombre >=5: ') Lire(n) Fin tant que # Retourner la valeur valide retourner n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La procédure remplir_fichier_nombre
Cette procédure a pour objectif de remplir un fichier texte "Nombre.txt" avec n entiers saisis par l’utilisateur.
Elle permet de créer un fichier texte contenant n entiers saisis par l’utilisateur, chaque entier sur une ligne séparée, prêt à être utilisé pour d’autres traitements (comme les tests de divisibilité).
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
Procedure remplir_fichier_nombre(n:entier) Ecrire('*** Remplir fichier Nombre.txt ***') # Ouverture du fichier en écriture Ouvrir(f =, "Nombre.txt", "w") # Saisie et écriture des entiers dans le fichier Pour i de 0 à n-1 faire Ecrire('donner un entier: ') Lire(nbr) Ecrire(f, nbr + '\n') # Chaque entier est écrit sur une nouvelle ligne Fin pour # Fermeture du fichier Fermer(f) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| f | fichier |
| i | entier |
| nbr | chaîne |
La fonction divis7
Cette fonction permet de vérifier si un nombre est divisible par 7 en utilisant une méthode spéciale basée sur une série répétitive [1, 3, 2, -1, -3, -2].
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
Fonction divis7(n:chaine, serie:tableau):booleen # Réduire le nombre à un chiffre par itérations Tant que long(n) != 1 faire s <- 0 k <- 0 Pour i de à long(n)-1 faire # Somme pondérée selon la série s <- s + Valeur(n[long(n)-1-i]) * serie[k] Si k < 5 alors k <- k + 1 Sinon k <- 0 Fin si Fin pour n <- Convch(s) # Réduire le nombre à la somme calculée Fin tant que # Vérification finale : divisible par 7 si résultat = 0 ou 7 Si (n = '7') ou (n = '0') alors retourner Vrai Sinon retourner Faux Fin si Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| s | entier |
| k | entier |
La procédure remplir_fichiers_div()
Cette procédure a pour objectif de lire les nombres du fichier "Nombre.txt" et de créer deux fichiers distincts :
"Div13.txt" → pour les nombres divisibles par 13
"Div7.txt" → pour les nombres divisibles par 7
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
Procédure remplir_fichiers_div(): # Ouverture des fichiers Ouvrir(f_nbr , "Nombre.txt", "r") # Fichier source Ouvrir(f_div13 , "Div13.txt", "w") # Fichier pour les nombres divisibles par 13 Ouvrir(f_div7 , "Div7.txt", "w") # Fichier pour les nombres divisibles par 7 # Lecture de tous les nombres nombres <- Lire_lignes(f_nbr) Pour nombre dans nombres faire nombre <- nombre.strip('\n') # Supprimer le saut de ligne Si divis13(nombre) alors # Vérifier divisibilité par 13 Ecrire(f_div13 , nombre + '\n') Fin si Si divis7(nombre, serie) alors # Vérifier divisibilité par 7 Ecrire(f_div7 , nombre + '\n') Fin si Fin pour # Fermeture des fichiers Fermer(f_nbr) Fermer(f_div13) Fermer(f_div7) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| f_nbr | fichier |
| f_div13 | fichier |
| f_div7 | fichier |
| nombres | chaîne |
| nombre | chaîne |
La procédure afficher_fichiers_div
Cette procédure permet de lire et d’afficher le contenu d’un fichier texte ligne par ligne.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
Procédure afficher_fichiers_div(nom_fichier:chaine) Ecrire('*** Contenu fichier ' + nom_fichier + ' ***') # Ouverture en lecture Ouvrir(f , nom_fichier , "r") nombres <- Lire_lignes(f) # Affichage ligne par ligne Pour nombre dans nombres faire nombre <- nombre.strip('\n') Ecrire(nombre) Fin pour # Fermeture du fichier Fermer(f) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| f | fichier |
| nombres | chaîne |
| nombre | chaîne |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 |
from numpy import * # -------------------------------------------------- # Création d'un tableau 'serie' de 100 entiers initialisés à 0 # Utilisé plus tard dans la fonction divis7 # -------------------------------------------------- serie = array([int()] * 100) # -------------------------------------------------- # Fonction qui saisit un entier n >= 5 # -------------------------------------------------- def saisie(): # Saisie initiale n = int(input('donner un nombre >=5: ')) # Vérification de la validité de la saisie while not (n >= 5): n = int(input('donner un nombre >=5: ')) # Retourner la valeur valide return n # -------------------------------------------------- # Procédure qui remplit le fichier "Nombre.txt" # avec n entiers saisis par l'utilisateur # -------------------------------------------------- def remplir_fichier_nombre(n): print('*** Remplir fichier Nombre.txt ***') # Ouverture du fichier en écriture f = open("Nombre.txt", "w") # Saisie et écriture des entiers dans le fichier for i in range(n): nbr = input('donner un entier: ') f.write(nbr + '\n') # Chaque entier est écrit sur une nouvelle ligne # Fermeture du fichier f.close() # -------------------------------------------------- # Fonction qui vérifie si un nombre est divisible par 13 # en utilisant une méthode de regroupement des 3 derniers chiffres # -------------------------------------------------- def divis13(n): s = 0 # Somme partielle sg = -1 # Alternance du signe (-1, +1) # Tant que le nombre a plus de 3 chiffres while len(n) > 3: # Prendre les 3 derniers chiffres v = int(n[len(n)-3:len(n)]) s = s + v * sg # Ajouter à la somme avec le signe sg = -sg # Inverser le signe pour la prochaine tranche n = n[0:len(n)-3] # Retirer les 3 derniers chiffres # Ajouter les chiffres restants v = int(n) s = s + v * sg # Retourner True si divisible par 13, False sinon return abs(s) % 13 == 0 # -------------------------------------------------- # Fonction qui vérifie si un nombre est divisible par 7 # en utilisant la série [1,3,2,-1,-3,-2] de manière répétitive # -------------------------------------------------- def divis7(n, serie): # Réduire le nombre à un chiffre par itérations while len(n) != 1: s = 0 k = 0 for i in range(len(n)): # Somme pondérée selon la série s = s + int(n[len(n)-1-i]) * serie[k] if k < 5: k = k + 1 else: k = 0 n = str(s) # Réduire le nombre à la somme calculée # Vérification finale : divisible par 7 si résultat = 0 ou 7 if n == '7' or n == '0': return True else: return False # -------------------------------------------------- # Procédure qui remplit les fichiers "Div13.txt" et "Div7.txt" # -------------------------------------------------- def remplir_fichiers_div(): # Ouverture des fichiers f_nbr = open("Nombre.txt", "r") # Fichier source f_div13 = open("Div13.txt", "w") # Fichier pour les nombres divisibles par 13 f_div7 = open("Div7.txt", "w") # Fichier pour les nombres divisibles par 7 # Lecture de tous les nombres nombres = f_nbr.readlines() for nombre in nombres: nombre = nombre.strip('\n') # Supprimer le saut de ligne if divis13(nombre): # Vérifier divisibilité par 13 f_div13.write(nombre + '\n') if divis7(nombre, serie): # Vérifier divisibilité par 7 f_div7.write(nombre + '\n') # Fermeture des fichiers f_nbr.close() f_div13.close() f_div7.close() # -------------------------------------------------- # Procédure qui affiche le contenu d'un fichier # -------------------------------------------------- def afficher_fichiers_div(nom_fichier): print('*** Contenu fichier ' + nom_fichier + ' ***') # Ouverture en lecture f = open(nom_fichier, "r") nombres = f.readlines() # Affichage ligne par ligne for nombre in nombres: nombre = nombre.strip('\n') print(nombre) # Fermeture du fichier f.close() # -------------------------------------------------- # Initialisation de la série utilisée pour divis7 # -------------------------------------------------- serie[0] = 1 serie[1] = 3 serie[2] = 2 serie[3] = -1 serie[4] = -3 serie[5] = -2 # -------------------------------------------------- # Programme principal # -------------------------------------------------- n = saisie() # Saisie du nombre d'entiers remplir_fichier_nombre(n) # Remplissage du fichier Nombre.txt remplir_fichiers_div() # Remplissage des fichiers Div13.txt et Div7.txt afficher_fichiers_div("Div13.txt") # Affichage des nombres divisibles par 13 afficher_fichiers_div("Div7.txt") # Affichage des nombres divisibles par 7 |
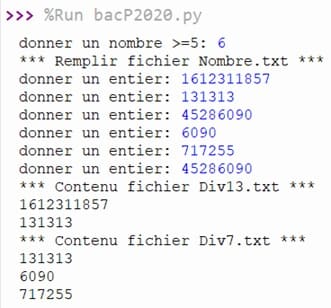
Exécution du programme
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés