Produit des diviseurs version 2 – Bac Pratique 2016 [ Algorithme + Python ]

Sujet bac informatique pratique 2017 (Bac scientifique)
Etant donné un entier N qui vérifie la propriété suivante : Le produit des diviseurs de n sauf lui-même est égale à une puissance de n avec un exposant > 0
Exemples :
N=6 vérifie cette propriété car le produit de ses diviseurs sauf lui-même est égal à 6 (1*2*3=6) qui est une puissance de 6, avec un exposant =1(car 6=61)
N=12 vérifie cette propriété car le produit de ses diviseurs sauf lui-même est égal à 144 (1*2*3*4*6=144) qui est une puissance de 12, avec un exposant =2(car 144=122)
N=30 vérifie cette propriété car le produit de ses diviseurs sauf lui-même est égal à 27000 (1*2*3*5*6*10*15=27000) qui est une puissance de 30, avec un exposant =3(car 27000=303)
N=9 ne vérifie pas cette propriété car le produit de ses diviseurs sauf lui-même est égal à 3 (1*3=3) qui n’est pas une puissance de 9.
N=11 ne vérifie pas cette propriété car le produit de ses diviseurs sauf lui-même est égal à 1qui est une puissance de 11, avec un exposant égal à 0.
On se propose d’écrire un programme Python permettant de déterminer et d’afficher tous les nombres de [a,b] ( avec 2≤a≤b≤100) vérifiant la propriété donnée ci-dessus.
Solution Algorithmique
Pour résoudre ce problème, nous devons identifier les nombres dans l'intervalle [a,b] qui vérifient la propriété suivante : le produit de tous les diviseurs du nombre NN, sauf lui-même, est une puissance de NN avec un exposant strictement supérieur à 0.
Approche algorithmique :
1. Trouver les diviseurs d’un nombre N :
Pour chaque N, nous devons trouver tous ses diviseurs. Les diviseurs de N sont tous les nombres qui divisent N sans reste.
Ensuite, on exclut N lui-même de la liste des diviseurs.
2. Calculer le produit des diviseurs sauf N :
On calcule le produit de tous les diviseurs sauf N.
3. Vérifier si le produit est une puissance de N :
Le produit des diviseurs est une puissance de N si ce produit peut s'écrire sous la forme N exposant k, où k est un entier strictement supérieur à 0.
Pour vérifier cela, il suffit de diviser le produit par N de façon répétée jusqu'à ce que le résultat soit égal à 1. Si on atteint 1 en un nombre d'itérations k≥1, alors le produit est une puissance de N.
4. Parcourir tous les nombres dans l'intervalle [a,b] :
On parcourt tous les nombres de a à b et on applique la vérification ci-dessus pour chaque nombre.
Dans cet algorithme, On va utiliser deux fonctions et deux procédures :
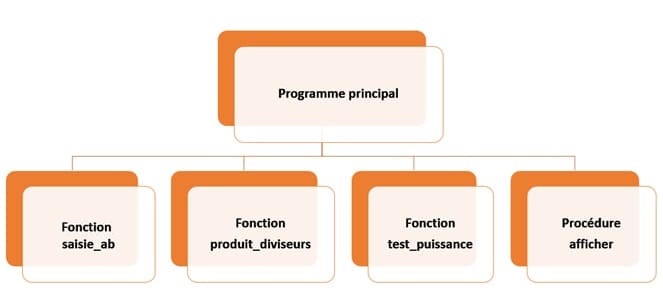
Algorithme du programme principal
|
1 2 3 4 5 |
Algorithme produits_diviseurs Debut saisie_ab() afficher(a,b) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| a | entier |
| b | entier |
La procédure saisie_ab
Cette procédure saisit deux entiers a et b tel que 2 ≤ a < b ≤ 100
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
Procedure saisie_ab(): Début Ecrire('donner un entier a entre 2 et 100:') lire (a) Tant que a<2 ou a>100 faire Ecrire('donner un entier a entre 2 et 100:') lire (a) Fin tant que Ecrire('donner un entier b tq "+a+"<b<=100: ') lire (b) Tant que b<a ou b>100 faire Ecrire('donner un entier b tq "+a+"<b<=100: ') lire (b) Fin tant que Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| a | entier |
| b | entier |
La fonction produit_diviseurs
Cette fonction calcule le produit des diviseurs de n sauf lui-même.
|
1 2 3 4 5 6 7 8 9 10 |
Fonction produit_diviseurs(n:entier):entier Début p<-1 Pour i de 1 à n div 2 faire Si (n div i =0) alors p<-p*i Finsi Fin pour retourner p Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| p | entier |
La fonction test_puissance
Cette fonction vérifie si le produit des diviseurs est une puissance de n
|
1 2 3 4 5 6 7 8 |
Fonction test_puissance(n:entier,m:entier):booleen Début p<-n Tant que (p<m) faire p<-p*n Fin tant que retourner p=m Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| p | entier |
La procédure afficher
Cette procédure affiche les nombres qui vérifient la propriété : "le produit des diviseurs de n sauf lui-même est une puissance de n".
|
1 2 3 4 5 6 7 8 |
Procédure affiche(n:entier) Début Pour i de a à b faire Si (i=test_puissance(i,produit_diviseurs(i))) alors Ecrire(i) Fin si Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 |
def saisie_ab() : global a,b a=int(input("donner un entier a entre 2 et 100: ")) while(a<2) or (a>100) : a=int(input("donner un entier a entre 2 et 100: ")) b=int(input("donner un entier b tq "+str(a)+"<b<=100: ")) while(b<a) or (b>100) : b=int(input("donner un entier b tq "+str(a)+"<b<=100: ")) def produit_diviseurs(n): p=1; for i in range(1,(n//2) +1): if (n % i==0): p=p*i return p def test_puissance(n,m): p=n while (p<m) : p=p*n return p==m def afficher(a,b): for i in range(a,b+1): if (test_puissance(i,produit_diviseurs(i))): print(str(i)) # programme principal saisie_ab() afficher(a,b) |
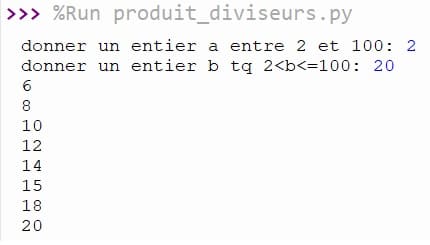
Exécution du programme
Solution en Python et Designer QT
Pour créer une application en Python pour afficher tous les nombres de l’intervalle [a,b] (avec 2 ≤ a < b ≤ 100), vérifiant la propriété donnée ci-dessus. en utilisant Qt Designer pour l'interface graphique, suivez ces étapes :
1- Créer l'interface graphique avec Qt Designer
a- Ouvrez Qt Designer et créez un nouveau fichier de type Main Window.
b- Ajoutez ces widgets:
QPushButton nommé 'afficher_bt' pour exécuter le module affichage().
QLabel nommé 'msg' pour afficher un message d'erreur
QLabel nommé 'resultat' pour afficher les nombres
QLineEdit nommé 'a' pour entrer un entier.
QLineEdit nommé 'b' pour entrer un entier.
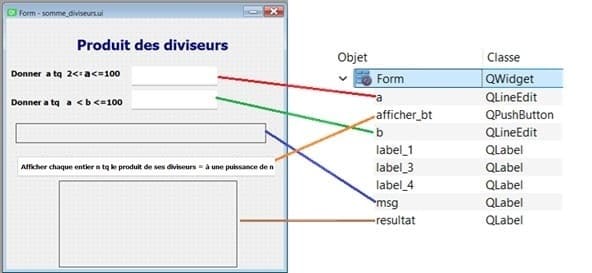
Enregistrez le fichier avec l'extension .ui, par exemple somme_diviseurs.ui.
2- Créer le script Python pour l'application
Voici un exemple de script Python qui utilise l'interface graphique générée par Qt Designer.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 |
from PyQt5.uic import loadUi from PyQt5 import QtCore, QtGui from PyQt5.QtWidgets import * from PyQt5 import QtCore, QtGui, QtWidgets app = QApplication([]) windows = loadUi ("produit_diviseurs.ui") def produit_diviseurs(n): p=1; for i in range(1,(n//2) +1): if (n % i==0): p=p*i return p def test_puissance(n,m): p=n while (p<m) : p=p*n return p==m def affichage(): a = int(windows.a.text()) b = int(windows.b.text()) cp=0 windows.msg.clear() if 2<=a<b<=100 : liste='' for i in range(a,b+1): if (test_puissance(i,produit_diviseurs(i))): liste=liste+str(i)+' ' cp=cp+1 if cp % 10 == 0: liste=liste+'\n' windows.resultat.setText(liste) else: windows.msg.setText('Veuillez saisir a et b tq 2<=a<b<=100') windows.afficher_bt.clicked.connect(affichage) windows.show() app.exec_() |
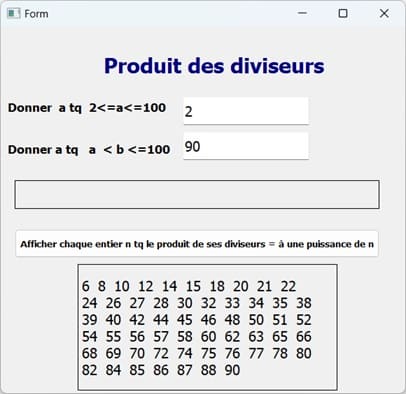
Exécution du programme
Vous pouvez voir aussi :
1) des exercices sur les chaînes des caractères
2) des exercices sur les tableaux
3) des sujets Bac pratique
4) des sujets Bac théorique
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés