Matrice – Bac pratique – Section informatique – 2014

Sujet (Algo et programmation - Bac 2014)
On se propose de remplir une matrice carrée M d'ordre N par des nombres premiers de l'intervalle [2, 99] et de rechercher les lignes et les colonnes de cette matrice dont les éléments sont ordonnés dans l'ordre croissant ou décroissant.
Exemple
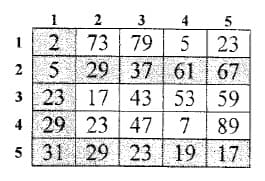
Pour la matrice carrée M d'ordre N=5 ci-dessus, les lignes et les colonnes dont les éléments sont ordonnés dans l'ordre croissant ou décroissant sont :
- La ligne 2 formée par les éléments 5 - 29 - 37 - 61 - 67
- La ligne 5 formée par les éléments 31 - 29 - 23 - 19 - 17
- La colonne 1 formée par les éléments 2 - 5 - 23 - 29 - 31
Travail demandé
Ecrire un programme en Python permettant de :
- remplir aléatoirement une matrice M d'ordre N donné (avec 4 < N < 20) par des nombres premiers de l'intervalle [2, 99].
- stocker dans chacune des lignes du fichier texte "Result.txt", la lettre "L" suivie par le numéro de la ligne de la matrice ou la lettre "C" suivie par le numéro de la colonne de la matrice M vérifiant la propriété citée ci-dessus, suivi d'un astérisque "*", suivi des éléments de cette ligne ou de cette colonne séparés par des tirets "-", comme le montre le formatage suivant :
Exemple pour la matrice M de l'exemple ci-dessus, le contenu du fichier "Result.txt" sera :
L2*5-29-37-61-67
L5*31-29-23-19-17
C1*2-5-23-29-31
Solution Algorithmique
Dans cet algorithme, On va utiliser sept fonctions et trois procédures:
- la fonction saisie()
- la fonction test_premier()
- la fonction saisie_element()
- la procédure remplir_matrice()
- la procédure afficher_matrice()
- la fonction test_ordonne_ligne()
- la fonction test_ordonne_colonne()
- la fonction elements_ligne()
- la fonction elements_colonne()
- la procédure remplir_fichier_result()
Algorithme du programme Principal
|
1 2 3 4 5 6 7 8 9 10 |
Algorithme eltpremier_matrice Debut Ecrire('*** Saisie du nombre des lignes et des colonnes ***') # Saisie de la dimension de la matrice n = saisie(3, 21) # Appel des différentes procédures remplir_matrice(m, n) afficher_matrice(m, n) remplir_fichier_result(m, n) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
| m | matrice |
La fonction saisie
La fonction saisie(inf, sup) permet de demander à l’utilisateur de saisir un entier strictement compris entre deux bornes inf et sup.
Plus précisément :
- La fonction affiche un message demandant un entier n tel que inf < n < sup. - Si la valeur saisie n’est pas dans l’intervalle ouvert ]inf, sup[, la saisie est redemandée. - La saisie est répétée tant que la condition n’est pas respectée. - Lorsque l’utilisateur entre enfin une valeur correcte, la fonction retourne cet entier.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
Fonction saisie():entier # Demande à l'utilisateur de saisir un entier n Ecrire('donner n tel que ' + inf + '< n < ' + sup + ': ') Lire(n) # Tant que n n'appartient pas à l'intervalle ]inf , sup[ # on redemande la saisie Tant que (n <= inf) ou (n >= sup) faire Ecrire('donner n tel que ' + inf + '< n < ' + sup + ': ') Lire(n) Fin tant que # Retourne la valeur correcte saisie retourner n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La fonction test_premier
Cette fonction sert à saisir et valider le nombre de colonnes d’une matrice en respectant trois contraintes :
La fonction saisie_colonne(inf, sup) :
1- Demande à l’utilisateur de saisir un entier n
2- Vérifie que n est : strictement supérieur à inf, strictement inférieur à sup et pair (divisible par 2)
3-Redemande la saisie tant que ces conditions ne sont pas respectées
4- Retourne la valeur valide de n
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
Fonction saisie_colonne():entier # Demande à l'utilisateur de saisir un entier n Ecrire('donner n pair tel que ' + inf + '< n < ' + sup + ': ') Lire(n) # Tant que n n'appartient pas à l'intervalle ]inf , sup[ # on redemande la saisie Tant que (n <= inf) ou (n >= sup) ou (m div 2 !=0) faire Ecrire('donner n pair tel que ' + inf + '< n < ' + sup + ': ') Lire(n) Fin tant que # Retourne la valeur correcte saisie retourner n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La fonction saisie_element
Cette fonction permet de tirer aléatoirement un entier premier compris entre 2 et 99 en s’appuyant sur une fonction de test de primalité.
1- La fonction commence par générer un entier aléatoire n entre 2 et 99.
2- Elle utilise la fonction test_premier(n) pour vérifier si n est un nombre premier.
3- Tant que n n’est pas premier, la fonction génère un nouveau nombre aléatoire.
4- Dès qu’un nombre premier est trouvé, la fonction le retourne.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
Fonction saisie_element():entier # Génération aléatoire d’un entier n entre 2 et 99 n <- Alea(2, 99) # Tant que le nombre généré n’est pas premier, # on génère un nouveau nombre aléatoire Tant que test_premier(n) = Faux faire n <- Alea(2, 99) Fin tant que # Retourne le nombre premier généré retourner n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La procédure remplir_matrice
Cette procédure permet de remplir une matrice carrée de taille n avec des nombres premiers générés aléatoirement.
1- La procédure affiche un message indiquant le début du remplissage de la matrice.
2- Elle parcourt la matrice ligne par ligne à l’aide de deux boucles imbriquées.
3- Pour chaque case m[i][j], elle appelle la fonction saisie_element().
4- La valeur retournée (un nombre premier compris entre 2 et 99) est affectée à la position correspondante de la matrice.
|
1 2 3 4 5 6 7 8 |
Procedure remplir_matrice(m:matrice, n:entier) Ecrire('*** Remplir la matrice M ***') Pour i de 0 à n-1 faire Pour j de 0 à n-1 faire m[i][j] <- saisie_element() Fin pour Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| j | entier |
La procédure afficher_matrice
Cette procédure permet d’afficher les éléments d’une matrice carrée M de taille n.
1- La procédure affiche un message indiquant l’affichage de la matrice.
2- Elle parcourt la matrice ligne par ligne à l’aide de deux boucles imbriquées.
3- Les éléments d’une même ligne sont affichés sur la même ligne, séparés par des espaces.
4- Après chaque ligne, un retour à la ligne est effectué pour conserver la forme matricielle.
|
1 2 3 4 5 6 7 8 9 |
Procedure afficher_matrice(m:matrice, n:entier) Ecrire(''*** Contenu de la matrice M ***'') Pour i de 0 à n-1 faire Pour j de 0 à n-1 faire Ecrire(m[i][j],' ') Fin pour Ecrire() Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| j | entier |
La fonction test_ordonne_ligne
Cette fonction permet de déterminer si une ligne donnée d’une matrice est totalement ordonnée (croissante ou décroissante).
1- La fonction teste d’abord si la ligne i est strictement croissante :
Elle compare chaque élément avec le suivant (m[i][j] < m[i][j+1]). Si cette relation est vérifiée pour toute la ligne, la fonction retourne True. Si la ligne n’est pas croissante, la fonction teste alors si elle est strictement décroissante : Elle compare chaque élément avec le suivant (m[i][j] > m[i][j+1]).
2- Si cette condition est vérifiée pour toute la ligne, la fonction retourne Vrai.
3- Si la ligne n’est ni croissante ni décroissante, la fonction retourne Faux.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
Fonction test_ordonne_ligne(m:matrice, i:entier, n:entier):booleen j <- 0 # Test de l’ordre croissant Tant que (j < n - 2) et (m[i][j] < m[i][j + 1]) faire j <- j + 1 Fin tant que Si (m[i][j] < m[i][j + 1]) alors retourner Vrai Sinon j <- 0 # Test de l’ordre décroissant Tant que (j < n - 2) and (m[i][j] > m[i][j + 1]) faire j <- j + 1 Fin tant que retourner (m[i][j] > m[i][j + 1]) Fin si Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| j | entier |
La fonction test_ordonne_colonne
Cette fonction permet de déterminer si une colonne donnée d’une matrice est totalement ordonnée (croissante ou décroissante).
1- La fonction teste d’abord si la colonne j est strictement croissante :
2- Elle compare chaque élément avec celui qui se trouve juste en dessous
(m[i][j] < m[i+1][j]). Si cette relation est vérifiée pour toute la colonne, la fonction retourne True. Si la colonne n’est pas croissante, la fonction teste alors si elle est strictement décroissante : Elle compare chaque élément avec le suivant (m[i][j] > m[i+1][j]).
3- Si cette condition est vérifiée pour toute la colonne, la fonction retourne Vrai.
4- Si la colonne n’est ni croissante ni décroissante, la fonction retourne Faux.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
Fonction test_ordonne_colonne(m:matrice, j:entier, n:entier):booleen i <- 0 # Test de l’ordre croissant Tant que (i < n - 2) et (m[i][j] < m[i + 1][j]) faire i <- i + 1 Fin tant que Si (m[i][j] < m[i + 1][j]) alors retourner Vrai Sinon i <- 0 # Test de l’ordre décroissant Tant que (i < n - 2) et (m[i][j] > m[i + 1][j]) faire i <- i + 1 Fin tant que retourner (m[i][j] > m[i + 1][j]) Fin si Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| j | entier |
La fonction elements_ligne
Cette fonction permet de transformer les éléments d’une ligne d’une matrice en une chaîne de caractères séparée par des tirets.
1- La fonction initialise une chaîne vide liste.
2- Elle parcourt tous les éléments de la ligne i.
3- Chaque élément est converti en chaîne de caractères et ajouté à liste, suivi d’un tiret.
4- À la fin, le dernier tiret est supprimé.
5- La chaîne finale est retournée.
|
1 2 3 4 5 6 7 |
Fonction elements_ligne(m:matrice, i:entier, n:entier):chaine liste <- '' Pour j de 0 à n-1 faire liste <- liste + Convch(m[i][j]) + '-' Fin pour retourner Sous_chaine(liste , 0 , long(liste)-1] Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| j | entier |
| liste | chaîne |
La fonction elements_colonne
Cette fonction permet de transformer les éléments d’une colonne d’une matrice en une chaîne de caractères séparée par des tirets.
1- La fonction initialise une chaîne vide liste.
2- Elle parcourt tous les éléments de la colonne j.
3- Chaque élément est converti en chaîne de caractères et ajouté à liste, suivi d’un tiret.
4- À la fin, le dernier tiret est supprimé.
5- La chaîne obtenue est retournée.
|
1 2 3 4 5 6 7 |
Fonction elements_colonne(m:matrice, j:entier, n:entier):chaine liste <- '' Pour i de 0 à n-1 faire liste <- liste + Convch(m[i][j]) + '-' Fin pour retourner Sous_chaine(liste , 0 , long(liste)-1] Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| j | entier |
| liste | chaîne |
La procédure remplir_fichier_result
Cette procédure remplir_fichier_long_seq(t, longueur_tableau, max_sequence) a pour rôle de créer et remplir le fichier texte Long_Seq.txt avec les informations relatives aux plus longues séquences d’éléments juxtaposés dont la somme est égale à zéro.
Détail du fonctionnement :
Elle ouvre (ou crée) le fichier Long_Seq.txt en mode écriture.
Elle écrit dans la première ligne du fichier le nombre d’éléments de la plus longue séquence trouvée.
Elle parcourt ensuite le tableau T, qui contient toutes les séquences détectées.
Pour chaque séquence, elle calcule sa longueur à partir des indices de début (icd) et de fin (icf).
Si la longueur de la séquence correspond à la longueur maximale (max_sequence), ses informations sont :
affichées à l’écran,
enregistrées dans le fichier sous la forme : NL#ICD#ICF.
Enfin, le fichier est fermé correctement.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
Procédure remplir_fichier_result(m:matrice, n:entier) Ecrire('*** Contenu du fichier Result.txt ***') Ouvrir(f , "Result.txt", "w") # Traitement des lignes Pour i de 0 à n-1 faire Si test_ordonne_ligne(m, i, n) alors Ecrire(f, 'L' + str(i) + '*' + elements_ligne(m, i, n) + '\n') Ecrire('L' + str(i) + '*' + elements_ligne(m, i, n)) Fin si Fin pour # Traitement des colonnes Pour j de 0 à n-1 faire Si test_ordonne_colonne(m, j, n) alors Ecrire(f , 'C' + str(j) + '*' + elements_colonne(m, j, n) + '\n') Ecrire('C' + str(j) + '*' + elements_colonne(m, j, n)) Fin si Fin pour Fermer(f) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| f | fichier |
| i | entier |
| j | entier |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 |
from numpy import * # -------------------------------------------------- # Définition des dimensions maximales de la matrice # -------------------------------------------------- lignes = 50 # Nombre maximal de lignes colonnes = 50 # Nombre maximal de colonnes # Création d'une matrice M de taille 50x50 initialisée à 0 m = array([[int()] * colonnes] * lignes) # -------------------------------------------------- # Fonction qui permet de saisir un entier n # compris strictement entre inf et sup # -------------------------------------------------- def saisie(inf, sup): # Demande à l'utilisateur de saisir un entier n = int(input('donner n tel que ' + str(inf) + '< n < ' + str(sup) + ': ')) # Tant que n n’appartient pas à l’intervalle ]inf , sup[ # on redemande la saisie while (n <= inf) or (n >= sup): n = int(input('donner n tel que ' + str(inf) + '< n < ' + str(sup) + ': ')) # Retourne la valeur valide return n # -------------------------------------------------- # Fonction qui teste si un entier n est premier # -------------------------------------------------- def test_premier(n): # Cas particulier : 2 est un nombre premier if n != 2: i = 2 # Recherche d’un diviseur entre 2 et n//2 while (i < n // 2) and (n % i != 0): i = i + 1 # n est premier s'il n'a aucun diviseur return (n % i != 0) else: return True # -------------------------------------------------- # Fonction qui génère et retourne un entier premier # compris entre 2 et 99 # -------------------------------------------------- def saisie_element(): # Génération aléatoire d’un entier n entre 2 et 99 n = random.randint(2, 99) # Tant que le nombre généré n’est pas premier, # on génère un nouveau nombre aléatoire while test_premier(n) == False: n = random.randint(2, 99) # Retourne le nombre premier généré return n # -------------------------------------------------- # Procédure qui remplit la matrice M # avec des nombres premiers # -------------------------------------------------- def remplir_matrice(m, n): print('*** Remplir la matrice M ***') for i in range(n): for j in range(n): m[i][j] = saisie_element() # -------------------------------------------------- # Procédure qui affiche la matrice M # -------------------------------------------------- def afficher_matrice(m, n): print('*** Contenu de la matrice M ***') for i in range(n): for j in range(n): print(m[i][j], end=' ') print() # -------------------------------------------------- # Fonction qui vérifie si une ligne est # entièrement croissante ou décroissante # -------------------------------------------------- def test_ordonne_ligne(m, i, n): j = 0 # Test de l’ordre croissant while (j < n - 2) and (m[i][j] < m[i][j + 1]): j = j + 1 if (m[i][j] < m[i][j + 1]): return True else: j = 0 # Test de l’ordre décroissant while (j < n - 2) and (m[i][j] > m[i][j + 1]): j = j + 1 return (m[i][j] > m[i][j + 1]) # -------------------------------------------------- # Fonction qui vérifie si une colonne est # entièrement croissante ou décroissante # -------------------------------------------------- def test_ordonne_colonne(m, j, n): i = 0 # Test de l’ordre croissant while (i < n - 2) and (m[i][j] < m[i + 1][j]): i = i + 1 if (m[i][j] < m[i + 1][j]): return True else: i = 0 # Test de l’ordre décroissant while (i < n - 2) and (m[i][j] > m[i + 1][j]): i = i + 1 return (m[i][j] > m[i + 1][j]) # -------------------------------------------------- # Fonction qui retourne les éléments d’une ligne # sous forme de chaîne de caractères # -------------------------------------------------- def elements_ligne(m, i, n): liste = '' for j in range(n): liste = liste + str(m[i][j]) + '-' return liste[0:len(liste) - 1] # -------------------------------------------------- # Fonction qui retourne les éléments d’une colonne # sous forme de chaîne de caractères # -------------------------------------------------- def elements_colonne(m, j, n): liste = '' for i in range(n): liste = liste + str(m[i][j]) + '-' return liste[0:len(liste) - 1] # -------------------------------------------------- # Procédure qui remplit le fichier Result.txt # avec les lignes et colonnes ordonnées # -------------------------------------------------- def remplir_fichier_result(m, n): print('*** Contenu du fichier Result.txt ***') f = open("Result.txt", "w") # Traitement des lignes for i in range(n): if test_ordonne_ligne(m, i, n): f.write('L' + str(i) + '*' + elements_ligne(m, i, n) + '\n') print('L' + str(i) + '*' + elements_ligne(m, i, n)) # Traitement des colonnes for j in range(n): if test_ordonne_colonne(m, j, n): f.write('C' + str(j) + '*' + elements_colonne(m, j, n) + '\n') print('C' + str(j) + '*' + elements_colonne(m, j, n)) f.close() # -------------------------------------------------- # Programme principal # -------------------------------------------------- print('*** Saisie du nombre des lignes et des colonnes ***') # Saisie de la dimension de la matrice n = saisie(3, 21) # Appel des différentes procédures remplir_matrice(m, n) afficher_matrice(m, n) remplir_fichier_result(m, n) |
Exécution du programme

0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés