Nombre Nrond – Bac théorique – Section informatique – 2024

Sujet (Algo et programmation - Bac 2024)
On se propose de vérifier si un entier M, supérieur ou égal à 2, est n-rond.
M est dit n-rond s’il existe un entier n tel que le plus grand facteur premier de M, noté P, vérifie la condition 𝑃 ≤ 𝑛√𝑀 (avec 𝑛√𝑀 est la racine nième de M).
Afin de calculer une valeur approchée de la racine nième de M (n√M), on utilise la suite 𝑥 définie comme suit :
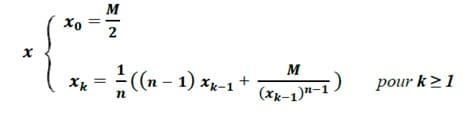
Travail demandé :
1- Ecrire un algorithme d’une fonction RacineN (M , n) qui permet de retourner une valeur approchée de la racine nième de M, en utilisant la suite 𝑥. Le calcul s’arrête lorsque | 𝑥 k – 𝑥 k-1 | ≤ 10-4 et la valeur approchée de 𝑛√𝑀 correspond alors au dernier terme calculé 𝑥 k.
2- Ecrire un algorithme d’une fonction Facteur (M) qui permet de retourner le plus grand facteur premier P de l’entier M.
Exemples :
Pour M=21 la fonction Facteur retourne 7 car sa décomposition en facteurs premiers donne 21 = 3 * 7.
Pour M=432 la fonction Facteur retourne 3 car sa décomposition en facteurs premiers donne 432 = 24 * 33.
3- En faisant appel aux deux fonctions RacineN et Facteur, écrire un algorithme d’une fonction NRond (M) qui permet de retourner le plus grand entier n qui vérifie 𝑃 ≤ 𝑛√𝑀 dans le cas où M est n-rond et de retourner -1 dans le cas contraire (avec P est le plus grand facteur premier de M).
Exemples :
NRond (432) retourne 5 car pour P=3, qui est le plus grand facteur premier de 432, l’entier n=5 correspond au plus grand entier qui vérifie 3 ≤ 5√432. En effet on a :
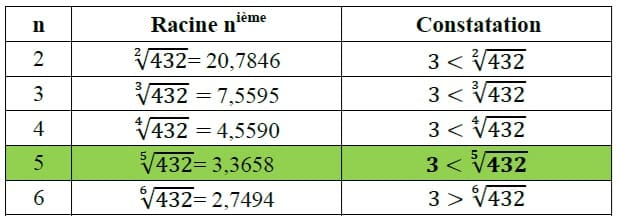
NRond (21) retourne -1 car pour P=7, qui est le plus grand facteur premier de 21, il n’existe pas un entier n tel que 7 < n√21 .
En effet 7 > 2√21 = 4,5825.
Solution Algorithmique
Dans cet algorithme, On va utiliser cinq fonctions :
- la fonction saisie()
- la fonction exposant()
- la fonction racine()
- la fonction facteur()
- la fonction nrond()
Algorithme du programme Principal
|
1 2 3 4 5 6 7 8 9 10 |
Algorithme nombre_nrond Debut m <- saisie() # Saisie de l'entier par l'utilisateur # Test si m est "Nrond" Si nrond(m) != -1 alors Ecrire(m, 'est Nrond') Sinon Ecrire(m, 'est non Nrond') Finsi Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| m | entier |
La fonction saisie
Cette fonction permet de saisir et retourner un entier > 2 en contrôlant la validité de la saisie.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
Fonction saisie():entier # Demande à l'utilisateur de saisir un entier n > 2 Ecrire('donner un entier n > 2') Lire(n) # Vérification de la validité de la saisie Tant que Non (n > 2) faire Ecrire('donner un entier n > 2 : ') Lire(n) Fin tant que # Retourne la valeur valide saisie par l'utilisateur retourner n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
La fonction exposant
Cette fonction calcule et retourne la valeur de ne en utilisant des multiplications successives.
|
1 2 3 4 5 6 7 8 |
Fonction exposant(n:entier , e:entier):entier exp <- 1 # Multiplication répétée n * n * ... * n (e fois) Pour i de 0 à e-1 faire exp <- exp * n Fin pour retourner exp Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| exp | entier |
La fonction racine
Cette fonction calcule la racine n-ième d’un nombre m par itérations successives et retourne la valeur approchée de la racine.
|
1 2 3 4 5 6 7 8 9 10 11 12 |
Fonction racine(m:entier, n:entier):reel x0 <- m / 2 # Valeur initiale approximative x1 <- (1/n) * ((n-1) * x0 + (m / exposant(x0, n-1))) # Première approximation # Boucle jusqu'à ce que la différence entre deux approximations soit < 0.0001 Tant que abs(x1 - x0) > 0.0001 faire x0 <- x1 x1 <- (1/n) * ((n-1) * x0 + (m / exposant(x0, n-1))) Fin tant que # Retourne la racine calculée retourner x1 Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| x0 | réel |
| x1 | réel |
La fonction facteur
Cette fonction permet de calculer le plus grand facteur premier d’un entier m.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
Fonction facteur(m:entier):entier i <- 2 grand_facteur <- 0 Tant que (m>1) faire Si m mod i = 0 alors # Si i divise m grand_facteur <- i m <- m div i # Divise m par i Sinon i <- i + 1 # Sinon, essaye le nombre suivant Fin si Fin tant que retourner grand_facteur Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| grand_facteur | entier |
La fonction nrond
Cette fonction permet de déterminer si un entier m est un nombre “Nrond” en utilisant la relation entre le plus grand facteur premier de m et ses racines n-ièmes.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
Fonction nrond(m:entier):booleen p <- facteur(m) # Plus grand facteur premier Ecrire("P=", p) n <- 3 r <- racine(m, n-1) # Calcul initial de la racine (n-1)-ième # Boucle jusqu'à ce que le plus grand facteur soit inférieur à la racine Tant que p < r faire Ecrire(r) n <- n+1 r <- racine(m, n) Fin tant que # Vérifie la condition finale pour retourner n ou -1 Si p <= racine(m, n-1) alors retourner n-1 Sinon retourner -1 Fin si Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| p | entier |
| r | réel |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 |
# -------------------------------------------------- # Fonction qui demande à l'utilisateur de saisir un entier n >= 2 # -------------------------------------------------- def saisie(): # Demande initiale à l'utilisateur m = int(input('donner n >= 2 : ')) # Vérification de la validité de la saisie # Tant que m est inférieur ou égal à 0, on redemande while not (m > 0): m = int(input('donner n >= 2 : ')) # Retourne la valeur valide saisie return m # -------------------------------------------------- # Fonction qui calcule n^e (puissance) # -------------------------------------------------- def exposant(n, e): exp = 1 # Multiplication répétée n * n * ... * n (e fois) for i in range(e): exp = exp * n return exp # -------------------------------------------------- # Fonction qui calcule la racine n-ième d'un nombre m # Méthode de Newton-Raphson # -------------------------------------------------- def racine(m, n): x0 = m / 2 # Valeur initiale approximative x1 = (1/n) * ((n-1) * x0 + (m / exposant(x0, n-1))) # Première approximation # Boucle jusqu'à ce que la différence entre deux approximations soit < 0.0001 while abs(x1 - x0) > 0.0001: x0 = x1 x1 = (1/n) * ((n-1) * x0 + (m / exposant(x0, n-1))) # Retourne la racine calculée return x1 # -------------------------------------------------- # Fonction qui calcule le plus grand facteur premier de m # -------------------------------------------------- def facteur(m): i = 2 grand_facteur = 0 while (m > 1): if m % i == 0: # Si i divise m grand_facteur = i m = m // i # Divise m par i else: i = i + 1 # Sinon, essaye le nombre suivant return grand_facteur # -------------------------------------------------- # Fonction qui détermine si m est un nombre "Nrond" # selon une propriété liée aux racines et au plus grand facteur premier # -------------------------------------------------- def nrond(m): p = facteur(m) # Plus grand facteur premier print("P=", p) n = 3 r = racine(m, n-1) # Calcul initial de la racine (n-1)-ième # Boucle jusqu'à ce que le plus grand facteur soit inférieur à la racine while p < r: print(r) n = n + 1 r = racine(m, n) # Vérifie la condition finale pour retourner n ou -1 if p <= racine(m, n-1): return n - 1 else: return -1 # -------------------------------------------------- # Programme principal # -------------------------------------------------- m = saisie() # Saisie de l'entier par l'utilisateur # Test si m est "Nrond" if nrond(m) != -1: print(m, 'est Nrond') else: print(m, 'est non Nrond') |
Exécution du programme
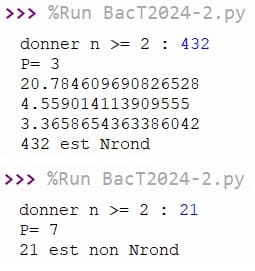
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés
























