Nombre Polydivisible – Bac Pratique 2014 [ Algorithme + Python ]

Sujet bac informatique pratique 2015 (Bac scientifique)
Un nombre Polydivisible est un entier naturel qui possède les propriétés suivantes :
1- Le nombre formé par ses deux premiers chiffres en allant de gauche à droite est un multiple de 2.
2- Le nombre formé par ses trois premiers chiffres en allant de gauche à doite est un multiple de 3.
3- Le nombre formé par ses quatre premiers chiffres en allant de gauche à doite est un multiple de 4.
4- etc.
Exemple 1: 345654 est un nombre Polydivisible en effet :
34 est un multiple de 2
345 est un multiple de 3
3456 est un multiple de 4
34565 est un multiple de 5
345654 est un multiple de 6
Exemple 2 : 12345 est un nombre non Polydivisible, parce que 1234 n’est pas un multiple de 4.
Travail demandé : écrire un programme Pascal qui permet de chercher et d’afficher tous les nombres Polydivisibles d’un intervalle [a,b] avec 100≤a Pour déterminer et afficher tous les nombres polydivisibles dans un intervalle [a,b] où 100≤a 1. Définition d'un nombre polydivisible Un nombre est polydivisible si, pour chaque sous-ensemble de ses premiers chiffres (en allant de gauche à droite), le nombre formé est divisible par sa longueur. 2. Parcours de l'intervalle [a,b] Parcourir chaque nombre nn dans l'intervalle [a,b]. 3. Vérification de la propriété polydivisible Pour chaque nombre n, vérifier si n est polydivisible : - Convertir le nombre en une chaîne de caractères pour accéder à ses chiffres. - Pour chaque sous-ensemble de chiffres ni allant de 2 à la longueur totale du nombre, vérifier que ni est divisible par sa longueur (par exemple, n2 est divisible par 2, n3 est divisible par 3, etc.). - Si toutes les vérifications sont réussies, le nombre est polydivisible. 4. Affichage des nombres polydivisibles Si un nombre est polydivisible, l'afficher. Dans cet algorithme, On va utiliser deux fonctions: Algorithme du programme principal Déclaration des objets Objet Type / Nature i entier n entier m entier La procédure saisie_nm Cette procédure saisit deux entiers m et n tel que 100≤n
Déclaration des objets Objet Type / Nature n entier m entier La fonction test_polydivisible Cette fonction calcule la somme des diviseurs propres de l'entier n excepté lui-même. Déclaration des objets Objet Type / Nature i entier n1 entier ch chaine des caracteres ch1 chaine des caracteres Exécution du programme Pour créer une application en Python pour afficher tous les nombres polydivisibles dans un intervalle [a,b] où 100≤a a- Ouvrez Qt Designer et créez un nouveau fichier de type Main Window. b- Ajoutez ces widgets: Enregistrez le fichier avec l'extension Voici un exemple de script Python qui utilise l'interface graphique générée par Qt Designer. Exécution du programme Vous pouvez voir aussi :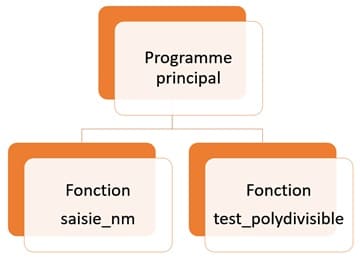
Solution en Python
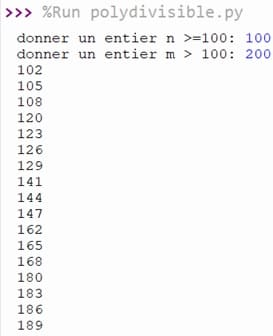
Solution en Python et Designer QT
1- Créer l'interface graphique avec Qt Designer
QLineEdit nommé 'n' pour entrer un entier >100.QLineEdit nommé 'm' pour entrer un entier >n>100.QPushButton nommé 'polydivisible_bt' pour exécuter le module recherche_polydivisible.QLabel nommé 'msg' pour afficher un message d'erreur.QLabel nommé 'resultat' pour afficher les nombres polydivisibles.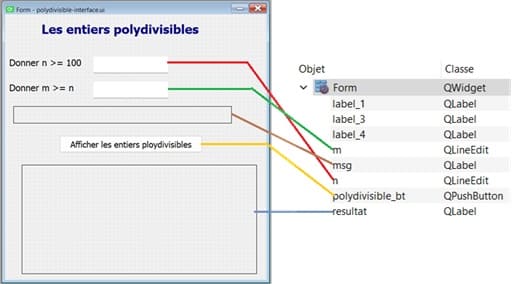
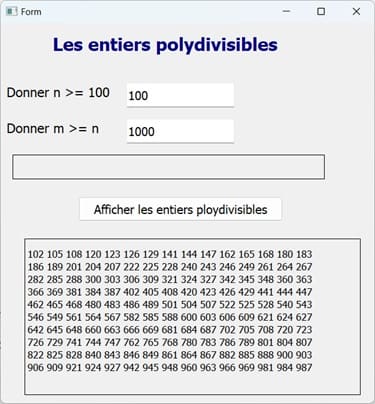
.ui, par exemple polydivisible-interface.ui.2- Créer le script Python pour l'application
1) des exercices sur les chaînes des caractères
2) des exercices sur les tableaux
3) des sujets Bac pratique
4) des sujets Bac théorique
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés