Nombres ronds – Bac informatique pratique scientifique 2025

Algo et Python 01-10-25

39 0

Sujet bac informatique pratique (Bac scientifique 2025)

On se propose de concevoir une interface graphique permettant de saisir deux entiers A et B tels que (10 ≤ A ≤ 30) et (A < B ≤ 99), puis d’afficher tous les nombres ronds compris entre A et B.

Un nombre est dit rond si sa conversion à la base 2 (base binaire) contient autant de 1 que de 0 (le nombre des 0 égal à celui des 1).

Exemples :

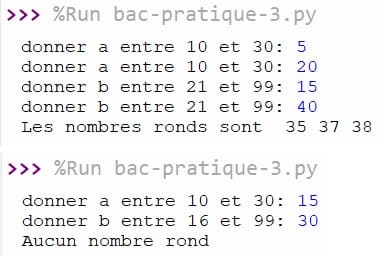
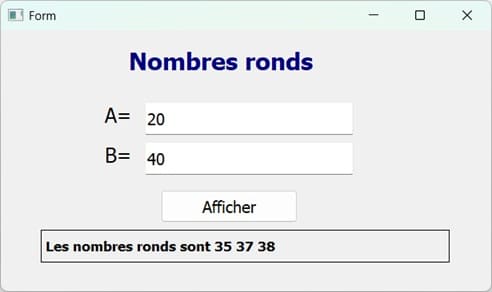
Pour A = 20 et B = 40 :

Le programme affiche : Les nombres ronds sont : 35-37-38

En effet, - la conversion binaire de 35₍₁₀₎ vaut 100011₍₂₎ qui contient autant de 1 que de 0.

la conversion binaire de 37₍₁₀₎ vaut 100101₍₂₎ qui contient autant de 1 que de
la conversion binaire de 38₍₁₀₎ vaut 100110₍₂₎ qui contient autant de 1 que de

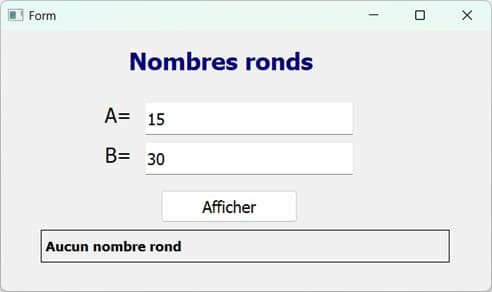
Pour A = 15 et B = 30 :

Il n’existe aucun nombre rond compris entre 15 et 30, d’où :

Le programme affiche : Aucun nombre rond

Solution Algorithmique

1- Saisie des bornes

Lire la valeur de A.

Lire la valeur de B.

Vérifier que : .

Si les conditions ne sont pas respectées → afficher un message d’erreur et redemander la saisie.

2- Parcours de l’intervalle

Pour chaque entier N allant de A à B (inclus) :

Convertir N en binaire.

Compter le nombre de 1 et le nombre de 0 dans cette représentation binaire.

3- Test de rondeur

Si le nombre de 1 = nombre de 0, alors :

Afficher N (c’est un nombre rond).

Sinon → ne rien afficher.

4- Fin de traitement

Lorsque tous les nombres de l’intervalle ont été testés, afficher un message indiquant la fin du programme.

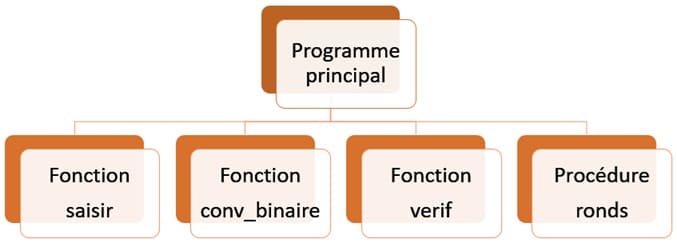
Dans cet algorithme, On va utiliser trois fonctions et une procédure :

Algorithme du programme Principal

Algorithme nombres_ronds
Debut
     a <- saisir('a',10,30)
     b <- saisir('b',a+1,99)
     ronds(a,b)
Fin

Algorithme nombres_ronds

Debut

a <- saisir('a',10,30)

b <- saisir('b',a+1,99)

ronds(a,b)

Fin

Déclaration des objets

Objet	Type / Nature
a	entier
b	entier

La fonction saisir

Cette fonction saisit un nombre entier N entre deux bornes

fonction saisie(variable,min,max):entier
Début
       Ecrire('donner ', variable ,' entre ', min ,' et ', str(max),': ')
       Lire(n)
       Tant que (n<min) ou (n>max) aire
           Ecrire('donner ', variable ,' entre ', min ,' et ', str(max),': ')
           Lire(n)
       Fin tant que
       retourner n
Fin

fonction saisie(variable,min,max):entier

Début

Ecrire('donner ', variable ,' entre ', min ,' et ', str(max),': ')

Lire(n)

Tant que (n<min) ou (n>max) aire

Ecrire('donner ', variable ,' entre ', min ,' et ', str(max),': ')

Lire(n)

Fin tant que

retourner n

Fin

Déclaration des objets

Objet	Type / Nature
n	entier

La fonction conv_binaire

Cette fonction permet de convertir un entier en binaire.

fonction conv_binaire(n:entier): chaine 
Début
      Si (n==0) alors
         ch <- "0"
      Sinon
         ch <- ""
      Tant que (n!=0) faire
        r <- n mod 2
        n <- n div 2
        ch <- Convh(r) + ch
      Fin tant que
      retourner ch 
Fin

fonction conv_binaire(n:entier): chaine

Début

Si (n==0) alors

ch <- "0"

Sinon

ch <- ""

Tant que (n!=0) faire

r <- n mod 2

n <- n div 2

ch <- Convh(r) + ch

Fin tant que

retourner ch

Fin

Déclaration des objets

Objet	Type / Nature
r	entier
ch	chaîne des caractères

La fonction verif

Cette fonction permet de vérifier si un entier est rond.

fonction verif(n:entier): booleen 
Début
     nbr_0 <- 0
     nbr_1 <- 0
     ch <- conv_binaire(n)
     pour i de 0 à long(ch)-1 faire
        Si ch[i]='0' alors
           nbr_0 <- nbr_0+1
        sinon
           nbr_1 <- nbr_1+1
        finsi
     finpour 
     Si nbr_0=nbr_1 alors
        retourner Vrai
     Sinon
        retourner Faux
     Finsi
Fin

fonction verif(n:entier): booleen

Début

nbr_0 <- 0

nbr_1 <- 0

ch <- conv_binaire(n)

pour i de 0 à long(ch)-1 faire

Si ch[i]='0' alors

nbr_0 <- nbr_0+1

sinon

nbr_1 <- nbr_1+1

finsi

finpour

Si nbr_0=nbr_1 alors

retourner Vrai

Sinon

retourner Faux

Finsi

Fin

Déclaration des objets

Objet	Type / Nature
nbr_0	entier
nbr_1	entier
ch	chaîne des caractères

La procédure ronds

Cette procédure recherche et affiche tous les nombres ronds compris entre A et B.

Procedure rond (a:entier;b:entier)
Début
     liste <- ""
     Pour i de a à b faire
       Si verif(i alors
          liste <- liste + Convch(i) + ' '
       Fin si
     Finpour
     Si long (liste) !=0 alors
       Ecrire ("Les nombres ronds sont ", liste)
     Sinon
       Ecrire("Aucun nombre rond")
     Fin si 
Fin

Procedure rond (a:entier;b:entier)

Début

liste <- ""

Pour i de a à b faire

Si verif(i alors

liste <- liste + Convch(i) + ' '

Fin si

Finpour

Si long (liste) !=0 alors

Ecrire ("Les nombres ronds sont ", liste)

Sinon

Ecrire("Aucun nombre rond")

Fin si

Fin

Déclaration des objets

Objet	Type / Nature
i	entier
liste	chaine

Solution en Python

def saisir(variable,min,max):
    n=int(input('donner '+ variable +' entre '+ str(min) +' et '+ str(max)+': '))
    while (n<min) or (n>max) :
        n=int(input('donner '+variable +' entre '+ str(min) +' et '+ str(max)+': '))
    return n

def conv_binaire(n):
    if (n==0) :
        ch="0"
    else:
        ch=""
        while (n!=0) :
            r= n % 2
            n= n // 2
            ch = str(r) + ch
    return ch            

def verif(n):
    nbr_0=0
    nbr_1=0
    ch=conv_binaire(n)
    for i in range(len(ch)):
        if ch[i]=='0' :
            nbr_0=nbr_0+1
        else :
            nbr_1=nbr_1+1
    if nbr_0==nbr_1 :
        return True
    else:
        return False

def ronds(a,b) :
    liste=""
    for i in range (a,b+1):
        if verif(i) :
           liste= liste + str(i) + ' '
    if len(liste) !=0 :
       print ("Les nombres ronds sont ", liste)
    else:
       print("Aucun nombre rond") 

#programme principal

a=saisir('a',10,30)
b=saisir('b',a+1,99)
ronds(a,b)

def saisir(variable,min,max):

n=int(input('donner '+ variable +' entre '+ str(min) +' et '+ str(max)+': '))

while (n<min) or (n>max) :

n=int(input('donner '+variable +' entre '+ str(min) +' et '+ str(max)+': '))

return n

def conv_binaire(n):

if (n==0) :

ch="0"

else:

ch=""

while (n!=0) :

r= n % 2

n= n // 2

ch = str(r) + ch

return ch

def verif(n):

nbr_0=0

nbr_1=0

ch=conv_binaire(n)

for i in range(len(ch)):

if ch[i]=='0' :

nbr_0=nbr_0+1

else :

nbr_1=nbr_1+1

if nbr_0==nbr_1 :

return True

else:

return False

def ronds(a,b) :

liste=""

for i in range (a,b+1):

if verif(i) :

liste= liste + str(i) + ' '

if len(liste) !=0 :

print ("Les nombres ronds sont ", liste)

else:

print("Aucun nombre rond")

#programme principal

a=saisir('a',10,30)

b=saisir('b',a+1,99)

ronds(a,b)

Exécution du programme :

Solution en Python et Designer QT

Pour créer une application en Python et Designer QT afin de saisir deux entiers A et B tels que (10 ≤ A ≤ 30) et (A < B ≤ 99), puis d’afficher tous les nombres ronds compris entre A et B., on va suivre ces étapes:

1- Créer l'interface graphique avec Qt Designer

a- Ouvrez Qt Designer et créez un nouveau fichier de type Main Window.

b- Ajoutez ces widgets:

QLabel nommé 'msg' pour afficher les messages générés par le programme

QLineEdit nommé 'a' pour entrer le nombre A

QLineEdit nommé 'b' pour entrer le nombre B

QPushButton nommé 'afficher_bt' pour chercher et afficher tous les nombres ronds compris entre A et B

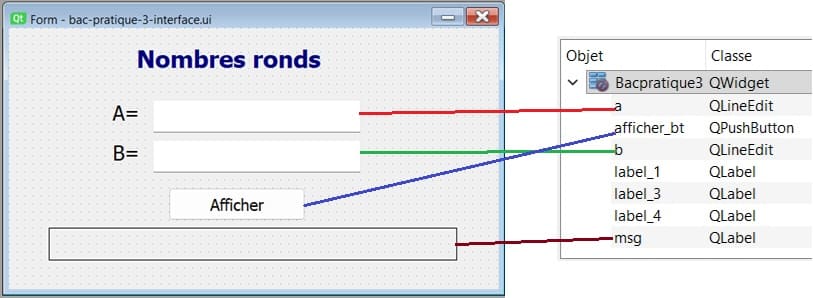
Enregistrez le fichier avec l'extension .ui, par exemple bac-pratique-3-interface.ui.ui.

2- Créer le script Python pour l'application

Voici un exemple de script Python qui utilise l'interface graphique générée par Qt Designer.

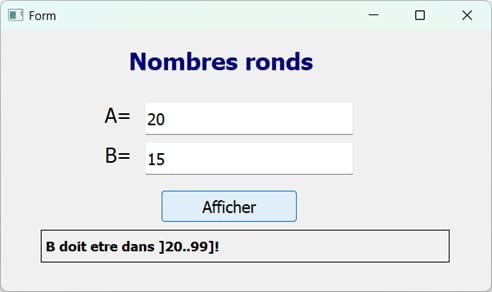
from PyQt5.uic import loadUi
from PyQt5.QtWidgets import QApplication

app = QApplication([])
windows = loadUi ("bac-pratique-3-interface.ui")

def conv_binaire(n):
    if (n==0) :
        ch="0"
    else:
        ch=""
        while (n!=0) :
            r= n % 2
            n= n // 2
            ch = str(r) + ch
    return ch            

def verif(n):
    nbr_0=0
    nbr_1=0
    ch=conv_binaire(n)
    for i in range(len(ch)):
        if ch[i]=='0' :
            nbr_0=nbr_0+1
        else :
            nbr_1=nbr_1+1
    if nbr_0==nbr_1 :
        return True
    else:
        return False
   
def play():
     windows.msg.clear() 
     a = int(windows.a.text())
     b = int(windows.b.text())
     
     if  (a>=10) and (a<=30):
       if  (b>a) and (b<=99):  
            liste=""
            for i in range (a,b+1):
                if verif(i) :
                   liste= liste + str(i) + ' '
            if len(liste) !=0 :
               windows.msg.setText("Les nombres ronds sont "+ str(liste))
            else:
               windows.msg.setText("Aucun nombre rond")
       else:
          windows.msg.setText('B doit etre dans ]'+str(a)+'..99]!' ) 
     else:        
        windows.msg.setText('A doit etre dans ]10..30]!' )
          
windows.afficher_bt.clicked.connect(play)

windows.show()
app.exec_()