Problème matrice – Bac théorique – Section informatique – 2011

Sujet (Algo et programmation - Bac 2011)
Soit Espace une matrice carrée d'ordre N remplie par des 0 et des 1. On se propose de Chercher les zones de concentration du chiffre 1 qui peuvent exister dans la matrice Espace. Pour déterminer les zones de concentration, on suit les étapes suivantes :
1- On remplit d'une manière aléatoire (au hasard) la matrice carrée Espace, par des 0 et des
2- On fixe DN, un diviseur de N, afin de partager la matrice Espace en carrés de dimensi DN*DN, comme l'illustre l'exemple suivant :
Si N = 9, et DN = 3 alors le nombre de carrés sera égal à
![]()
et la subdivision de la matrice Espace en 9 carrés se fera de la manière suivante :
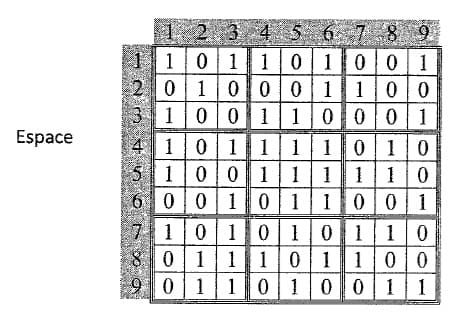
3- On saisit le degré de concentration minimum Deg_Min, pour lequel on va chercher zones de concentration du chiffre 1.
![]()
4- On détermine toutes les zones de concentration du chiffre 1 dans la matrice L s zones de concentration correspondent aux carrés de la matrice Espace qui contiennent n nombre d'occurrences du chiffre 1 supérieur ou égal à Deg_Min.
On se propose d'écrire un programMe qui permet de
- Saisir N, la taille de la matrice Espace et la remplir de 0 et de 1, d'une manière aléatoire. le Saisir DN, un diviseur de N.
- Saisir Deg_Min, le degré de concentration minimum (Deg_Min appartient à [1,(DN*DN)]).
- Déterminer et afficher le nombre de zones de concentration du chiffre 1.
- Afficher les caractéristiques de chaque zone de concentration en précisant à chaque fois les deux informations suivantes
1. Les coordonnées (ligne, colonne) de la lère case de la zone de concentration (en haut à gauche).
2. Le nombre d'occurrences du chiffre 1 figurant dans cette zone.
Pour la matrice Espace de l'exemple précédent et pour Deg_Min égal à 5, on obtient les résultats suivants :
Le nombre de zones de concentration du chiffre 1, est égal à 4.
Les zones de concentration se définissent ainsi :
Zone n'l : ligne : 1, colonne : 4. Le nombre de 1 dans cette zone est : 5.
Zone n°2 : ligne : 4, colonne : 4. Le nombre de 1 dans cette zone est : 8.
Zone n°3 : ligne : 7, colonne : 1. Le nombre de 1 dans cette zone est : 6.
Zone n°4 : ligne : 7, colonne : 7. Le nombre de 1 dans cette zone est : 5.
En effet, les zones de concentration étant les subdivisions de la matrice Espace où le n d'occurrences du chiffre 1 est supérieur ou égal à Deg_Min, on peut illustrer ces résultats manière suivante :
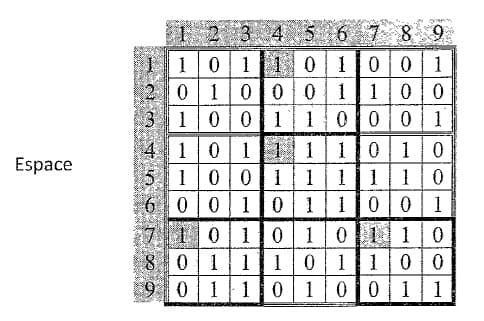
Travail demandé :
1- Analyser le problème en le décomposant en modules et en déduire l'algorithme du programme principal.
2- Analyser chacun des modules envisagés précédemment et en déduire les algorithmes correspondants.
Solution Algorithmique
Dans cet algorithme, On va utiliser quatre fonctions et trois procédures:
- la fonction saisie_n()
- la procédure remplir_matrice()
- la procédure afficher_matrice()
- la fonction saisie_dn()
- la fonction saisie_deg_min()
- la fonction nbr_occurences1()
- la procédure coordonnees_concentration()
Algorithme du programme Principal
|
1 2 3 4 5 6 7 8 9 10 11 |
Algorithme matrice_espace Debut n <- saisie_n() # Saisie de la taille de la matrice remplir_matrice(espace, n) # Remplissage aléatoire de la matrice Ecrire("**** Matrice Espace *****") afficher_matrice(espace, n) # Affichage de la matrice dn <- saisie_dn(n) # Saisie du diviseur deg_min <- saisie_deg_min(dn) # Saisie du degré minimum de concentration # Affichage des zones de concentration coordonnees_concentration(espace, dn, deg_min) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | entier |
| espace | matrice |
| dn | entier |
| deg_min | entier |
La fonction saisie_n
Cette procédure permet de saisir un entier compris strictement entre deux bornes inf et sup, en contrôlant la validité de la saisie.
Plus précisément :
il demande à l’utilisateur d’entrer un entier n tel que n >=4.
si la valeur saisie n’appartient pas à cet intervalle, le programme redemande la saisie jusqu’à obtenir une valeur correcte.
une fois la saisie valide, la fonction retourne l’entier n.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
Fonction saisie_n():entier # Première saisie de l'entier Ecrire('donner n telque n>=4: ') Lire(n) # Tant que n n'est pas dans l'intervalle demandé, # on redemande la saisie Tant que (n < 4) faire Ecrire('donner n telque n>=4: ') Lire(n) Fin tant que # Retourne la valeur correcte saisie retourner n Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| n | chaîne |
La procédure remplir_matrice
Cette procédure permet de remplir une matrice carrée m de taille n × n avec des valeurs aléatoires, où chaque élément prend soit la valeur 0, soit la valeur 1.
Plus précisément :
Elle parcourt toutes les lignes de la matrice de 0 à n-1.
Pour chaque ligne, elle parcourt toutes les colonnes de 0 à n-1.
À chaque position m[i][j], elle affecte un nombre aléatoire égal à 0 ou 1.
|
1 2 3 4 5 6 7 |
Procedure remplir_matrice(m:matrice ; n:entier) Pour i de 0 à n-1 faire Pour j de 0 à n-1 faire m[i][j] <- Alea(0, 1) Fin pour Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| j | entier |
La procédure afficher_matrice
Cette fonction permet d’afficher à l’écran une matrice carrée m de taille n × n, élément par élément, sous forme de tableau lisible.
Plus précisément :
Elle parcourt les lignes de la matrice de 0 à n-1.
Pour chaque ligne, elle parcourt toutes les colonnes.
Elle affiche chaque élément m[i][j] sur la même ligne, séparé par des espaces.
Après l’affichage d’une ligne complète, elle passe à la ligne suivante
|
1 2 3 4 5 6 7 8 |
Procedure afficher_matrice(m:matrice ; n:entier) Pour i de 0 à n-1 faire Pour j de 0 à n-1 faire Ecrire(m[i][j],' ') Fin pour Ecrire() Fin pour Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| j | entier |
La fonction saisie_dn
Cette fonction permet de saisir un entier dn qui est un diviseur du nombre n.
Plus précisément :
Elle demande à l’utilisateur de saisir un nombre dn.
Elle vérifie si dn divise exactement n (c’est-à-dire si le reste de la division n % dn est égal à 0).
Tant que dn n’est pas un diviseur de n, la saisie est redemandée.
Une fois un diviseur valide saisi, la fonction le retourne.
|
1 2 3 4 5 6 7 8 9 10 |
Fonction saisie_dn(n:entier):entier Ecrire('donner un diviseur de ' , n , ': ') Lire(dn) # Redemande la saisie tant que dn n’est pas un diviseur de n Tant que (n mod dn != 0) faire Ecrire('donner un diviseur de ' , n , ': ') Lire(dn) Fin tant que retourner dn Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| dn | entier |
La fonction saisie_deg_min
Cette fonction permet de saisir et de valider le degré de concentration minimum deg_min, c’est-à-dire le nombre minimal de valeurs égales à 1 exigé dans une zone de taille dn × dn.
Plus précisément :
Le programme demande à l’utilisateur de saisir un entier deg_min.
La valeur saisie doit appartenir à l’intervalle [1 , dn × dn], qui correspond au nombre maximum possible de cases dans une zone.
Tant que la valeur saisie n’est pas valide (inférieure à 1 ou supérieure à dn × dn), la saisie est redemandée.
Une fois une valeur correcte saisie, elle est retournée.
|
1 2 3 4 5 6 7 8 9 10 |
Fonction saisie_deg_min(dn:entier):entier Ecrire('donner le degré de concentration minimum appartient a [1 ,' , dn*dn , ']: ') Lire(deg_min) # Vérification de la validité de la saisie Tant que (deg_min < 1) ou (deg_min > dn*dn) faire Ecrire('donner le degré de concentration minimum appartient a [1 ,' , dn*dn , ']: ') Lire(deg_min) Fin tant que retourner deg_min Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| deg_min | entier |
La fonction nbr_occurences1
Cette fonction permet de calculer le nombre d’occurrences de la valeur 1 dans une sous-matrice de taille dn × dn de la matrice m.
Plus précisément :
La sous-matrice commence à la position (i, j) de la matrice m.
La fonction parcourt toutes les lignes de i à i + dn − 1.
Elle parcourt également toutes les colonnes de j à j + dn − 1.
À chaque case contenant la valeur 1, un compteur cp est incrémenté.
À la fin du parcours, le nombre total de 1 est retourné.
|
1 2 3 4 5 6 7 8 9 10 11 |
Fonction nbr_occurences1(m:matrice, i:entier, j:entier, dn:entier): entier cp <- 0 Pour k1 de i à i+dn-1 faire Pour k2 de j à j+dn-1 faire Si m[k1][k2] = 1 faire cp <- cp + 1 Fin si Fin pour Fin pour retourner cp Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| cp | entier |
| k1 | entier |
| k2 | entier |
La procédure coordonnees_concentration
Cette fonction permet d’identifier et d’afficher les zones de concentration du chiffre 1 dans la matrice m.
Plus précisément :
La matrice est découpée en sous-matrices de taille dn × dn.
La fonction parcourt chaque sous-matrice à l’aide des indices i et j.
Pour chaque zone, elle calcule le nombre de 1 en utilisant la fonction nbr_occurences1.
Si ce nombre est supérieur ou égal au degré de concentration minimum deg_min, la zone est considérée comme une zone de concentration.
Les coordonnées de la zone (ligne et colonne de départ) ainsi que le nombre de 1 sont affichées.
Un compteur numero_case permet de numéroter les zones trouvées.
À la fin, le programme affiche le nombre total de zones de concentration détectées.
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
Procédure coordonnees_concentration(m:matrice, dn:entier, deg_min:entier) numero_case <- 0 # Parcours des sous-matrices dn×dn Pour i de 0 à dn-1 faire Pour j de 0 à dn-1 faire # Calcul du nombre de 1 dans chaque zone If nbr_occurences1(m, i*dn, j*dn, dn) >= deg_min alors numero_case <- numero_case + 1 Ecrire("Zone N°" , numero_case , ": ligne:" , i*dn , ", colonne:" , j*dn , ". Le nombre de 1 est " , nbr_occurences1(m, i*dn, j*dn, dn)) Ecrire('*******************************************************') Ecrire('Le nombre de zones de concentration du chiffre 1 = ' , numero_case) Fin |
Déclaration des objets
| Objet | Type / Nature |
|---|---|
| i | entier |
| j | entier |
| numero_case | entier |
Solution en Python
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 |
from numpy import * import random # -------------------------------------------------- # Définition des dimensions maximales de la matrice # -------------------------------------------------- lignes = 50 colonnes = 50 # Matrice "espace" : # contiendra des valeurs 0 ou 1 représentant l’espace étudié espace = array([[int()] * colonnes] * lignes) # -------------------------------------------------- # Fonction qui permet de saisir un entier n tel que n >= 4 # -------------------------------------------------- def saisie_n(): n = int(input('donner nombre de lignes n telque n>=4: ')) # Redemande la saisie tant que n est inférieur à 4 while n < 4: n = int(input('donner nombre de lignes n telque n>=4: ')) return n # -------------------------------------------------- # Fonction qui remplit la matrice m de taille n×n # avec des valeurs aléatoires 0 ou 1 # -------------------------------------------------- def remplir_matrice(m, n): for i in range(n): for j in range(n): m[i][j] = random.randint(0, 1) # -------------------------------------------------- # Fonction qui affiche la matrice m de taille n×n # -------------------------------------------------- def afficher_matrice(m, n): for i in range(n): for j in range(n): print(m[i][j], end=' ') print() # -------------------------------------------------- # Fonction qui permet de saisir un diviseur dn de n # -------------------------------------------------- def saisie_dn(n): dn = int(input('donner un diviseur de ' + str(n) + ': ')) # Redemande la saisie tant que dn n’est pas un diviseur de n while n % dn != 0: dn = int(input('donner un diviseur de ' + str(n) + ': ')) return dn # -------------------------------------------------- # Fonction qui permet de saisir le degré de concentration minimum # Il doit appartenir à l’intervalle [1 , dn*dn] # -------------------------------------------------- def saisie_deg_min(dn): deg_min = int(input( 'donner le degré de concentration minimum appartient a [1 ,' + str(dn*dn) + ']: ')) # Vérification de la validité de la saisie while deg_min < 1 or deg_min > dn*dn: deg_min = int(input( 'donner le degré de concentration minimum appartient a [1 ,' + str(dn*dn) + ']: ')) return deg_min # -------------------------------------------------- # Fonction qui calcule le nombre de 1 # dans une sous-matrice de taille dn×dn # commençant à la position (i, j) # -------------------------------------------------- def nbr_occurences1(m, i, j, dn): cp = 0 for k1 in range(i, i + dn): for k2 in range(j, j + dn): if m[k1][k2] == 1: cp = cp + 1 return cp # -------------------------------------------------- # Fonction qui affiche les coordonnées des zones # où le nombre de 1 est supérieur ou égal à deg_min # -------------------------------------------------- def coordonnees_concentration(m, dn, deg_min): numero_case = 0 # Parcours des sous-matrices dn×dn for i in range(dn): for j in range(dn): # Calcul du nombre de 1 dans chaque zone if nbr_occurences1(m, i*dn, j*dn, dn) >= deg_min: numero_case = numero_case + 1 print("Zone N°" + str(numero_case) + ": ligne:" + str(i*dn) + ", colonne:" + str(j*dn) + ". Le nombre de 1 est " + str(nbr_occurences1(m, i*dn, j*dn, dn))) print('*******************************************************') print('Le nombre de zones de concentration du chiffre 1 = ' + str(numero_case)) # -------------------------------------------------- # Programme principal # -------------------------------------------------- n = saisie_n() # Saisie de la taille de la matrice remplir_matrice(espace, n) # Remplissage aléatoire de la matrice print("**** Matrice Espace *****") afficher_matrice(espace, n) # Affichage de la matrice dn = saisie_dn(n) # Saisie du diviseur deg_min = saisie_deg_min(dn) # Saisie du degré minimum de concentration # Affichage des zones de concentration coordonnees_concentration(espace, dn, deg_min) |
Exécution du programme
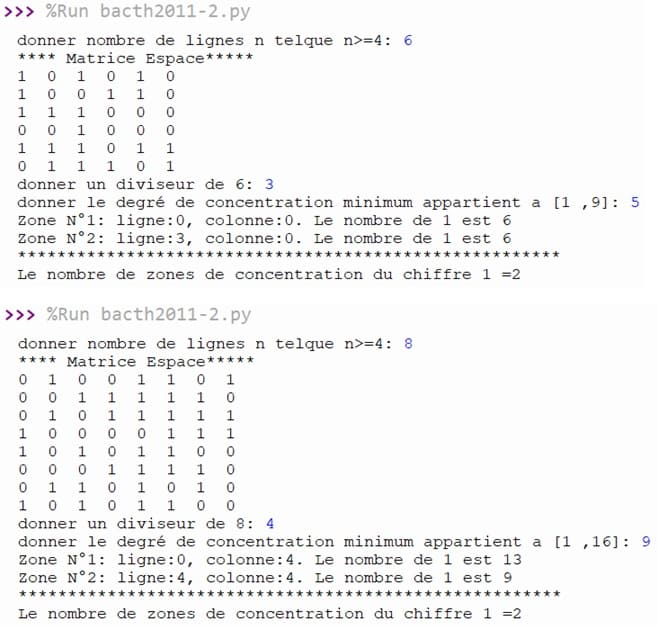
0 commentaire
laisser un commentaire
Tutoriels récents
Tutoriels populaires

Tutoriels plus commentés



















